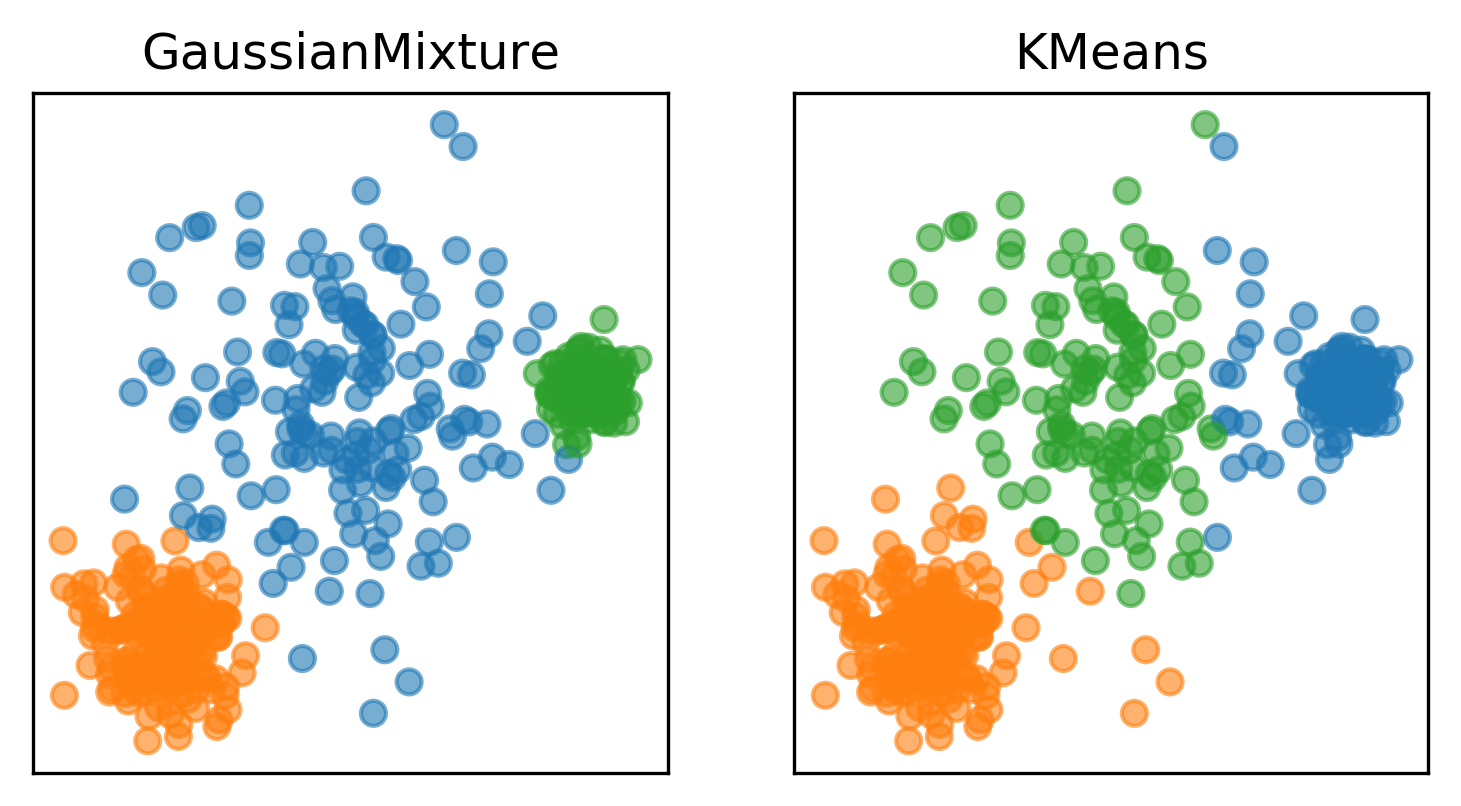
K-Means vs Gaussian Mixture Models: ¿cuál usar y para qué sirve cada uno?
Por Antonio Richaud, Publicado el 24 de Julio de 2024
En el mundo del machine learning y el análisis de datos, los algoritmos de clustering son herramientas fundamentales para descubrir patrones y estructuras ocultas en grandes volúmenes de datos. Estos algoritmos permiten agrupar elementos similares en "clusters" o grupos, facilitando la identificación de segmentos dentro de los datos que comparten características comunes. Esta capacidad es crucial en aplicaciones que van desde la segmentación de clientes en marketing hasta la identificación de patrones en la detección de fraudes.
Dos de los algoritmos de clustering más utilizados y conocidos son K-Means y Gaussian Mixture Models (GMM). Aunque ambos tienen como objetivo principal agrupar datos en clusters, lo hacen de formas muy distintas, y sus aplicaciones varían dependiendo de la naturaleza de los datos y los objetivos del análisis.
En este artículo, exploraremos en detalle cómo funcionan K-Means y Gaussian Mixture Models, sus ventajas y desventajas, y en qué casos es más conveniente utilizar uno u otro. A lo largo del artículo, también veremos ejemplos prácticos que ilustran cómo se comportan estos algoritmos en diferentes escenarios, lo que te permitirá tomar decisiones más informadas al seleccionar el método de clustering adecuado para tus proyectos.
Si alguna vez te has preguntado cuál es la diferencia entre estos dos algoritmos, cuándo deberías usar K-Means o cuándo GMM podría ser la mejor opción, este artículo es para ti. Al final de esta lectura, tendrás una comprensión clara de las fortalezas y limitaciones de cada algoritmo, así como de sus aplicaciones prácticas en el análisis de datos.
¿Qué es K-Means?
K-Means es uno de los algoritmos de clustering más populares y ampliamente utilizados en machine learning. Su simplicidad y eficiencia lo hacen ideal para una amplia variedad de aplicaciones, desde la segmentación de clientes hasta la agrupación de datos en biología computacional. El objetivo principal de K-Means es dividir un conjunto de datos en K grupos o "clusters", donde cada grupo contiene elementos que son más similares entre sí que a los elementos de otros grupos.
El funcionamiento de K-Means es iterativo y se basa en la minimización de la distancia entre los puntos de datos y el centroide de su cluster asignado. Este algoritmo comienza con la selección aleatoria de K centroides iniciales y luego asigna cada punto de datos al centroide más cercano. Después, recalcula la posición de los centroides como el promedio de todos los puntos asignados a cada uno, y repite este proceso hasta que los centroides no cambian significativamente, lo que indica que los clusters están estabilizados.
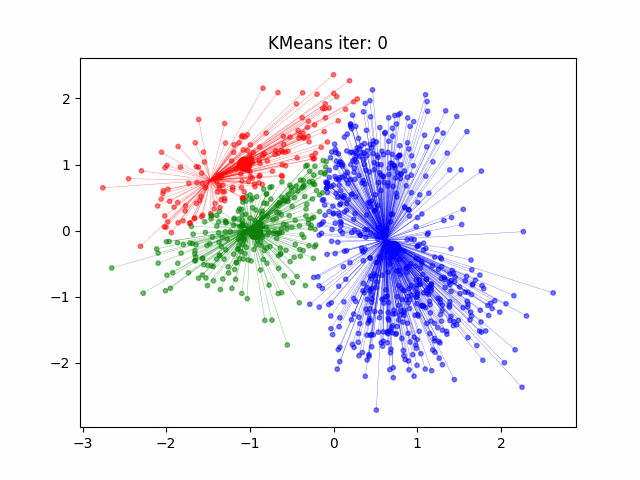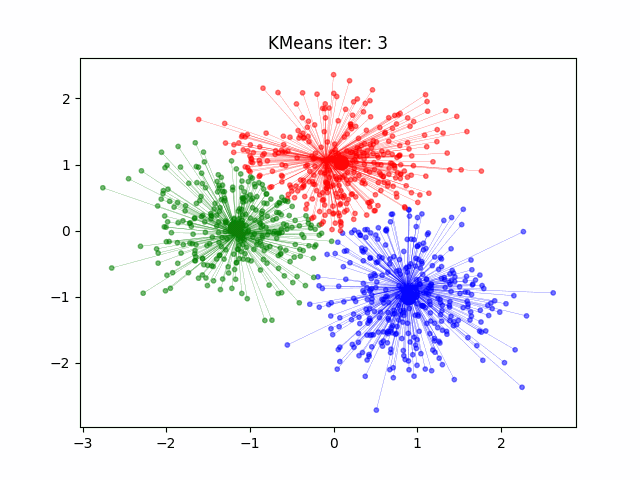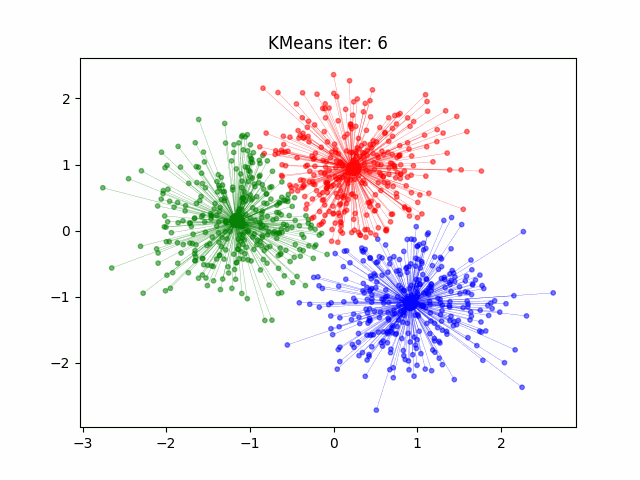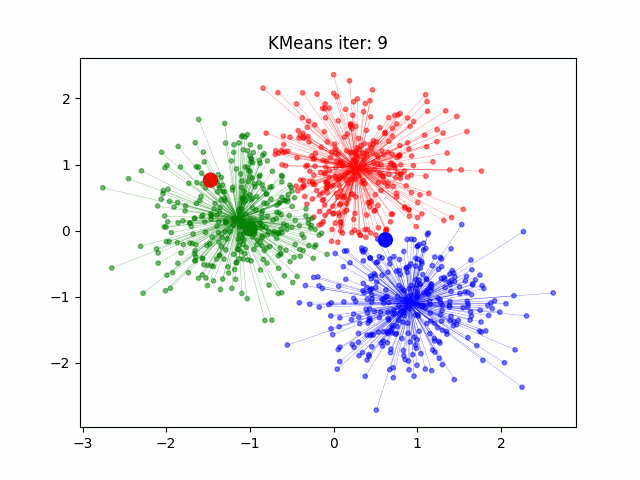
Podemos observar cómo K-Means agrupa datos en clusters. Comienza con la selección de centroides aleatorios y, a medida que avanza, los puntos de datos se reorganizan hasta que los centroides se estabilizan en posiciones óptimas. Este proceso se repite hasta que se minimiza la distancia dentro de cada cluster, resultando en una agrupación más coherente.
Aunque K-Means es rápido y fácil de implementar, tiene algunas limitaciones. Por ejemplo, asume que los clusters son esféricos y de tamaño similar, lo que puede no ser adecuado en todos los escenarios. Además, K-Means puede ser sensible a la inicialización de los centroides y puede converger a un mínimo local, lo que significa que los resultados pueden variar dependiendo de las condiciones iniciales.
Si estás interesado en una explicación más detallada sobre el funcionamiento de K-Means, te invito a consultar nuestro artículo dedicado a K-Means, donde exploramos este algoritmo en mayor profundidad, incluyendo ejemplos adicionales y consideraciones prácticas.
Ejemplo práctico de K-Means
Para ilustrar cómo funciona K-Means, vamos a usar un ejemplo simple con datos sintéticos. Imaginemos que tenemos un conjunto de datos bidimensionales que queremos agrupar en tres clusters. El siguiente código en Python muestra cómo implementar K-Means utilizando la biblioteca scikit-learn.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
# Generar datos sintéticos
np.random.seed(42)
X = np.vstack([
np.random.normal(loc=0.0, scale=1.0, size=(100, 2)),
np.random.normal(loc=5.0, scale=1.0, size=(100, 2)),
np.random.normal(loc=10.0, scale=1.0, size=(100, 2))
])
# Aplicar K-Means
kmeans = KMeans(n_clusters=3, random_state=42)
kmeans.fit(X)
y_kmeans = kmeans.predict(X)
# Visualizar los clusters
plt.scatter(X[:, 0], X[:, 1], c=y_kmeans, s=50, cmap='viridis')
centers = kmeans.cluster_centers_
plt.scatter(centers[:, 0], centers[:, 1], c='red', s=200, alpha=0.75)
plt.title('Clusters generados por K-Means')
plt.show()
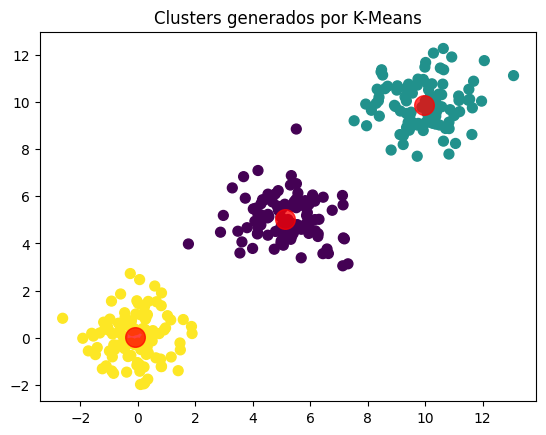
En este ejemplo, generamos tres grupos de datos bidimensionales y utilizamos K-Means para identificarlos. El gráfico resultante muestra los puntos de datos coloreados según el cluster al que pertenecen, y los centroides se destacan en rojo. K-Means ha logrado identificar los tres clusters de manera efectiva, agrupando puntos similares y separándolos de los diferentes.
¿Qué es Gaussian Mixture Models (GMM)?
Gaussian Mixture Models (GMM) es un enfoque probabilístico para el clustering que asume que los datos se distribuyen como una combinación de múltiples distribuciones gaussianas. A diferencia de K-Means, que asigna cada punto de datos a un solo cluster, GMM permite que un punto de datos pertenezca a varios clusters con diferentes probabilidades. Esto lo hace especialmente útil en situaciones donde los clusters tienen formas elípticas o cuando no tienen un tamaño uniforme.
GMM modela la distribución de los datos utilizando una suma ponderada de varias distribuciones gaussianas, cada una con su propia media y covarianza. El objetivo es encontrar los parámetros que mejor ajusten los datos a estas distribuciones, de manera que cada punto de datos tenga una probabilidad de pertenecer a cada cluster.
A continuación, veremos un ejemplo práctico que muestra cómo GMM puede identificar clusters en un conjunto de datos que no necesariamente tienen formas esféricas, lo cual sería un desafío para K-Means.
Ejemplo práctico de GMM
Vamos a utilizar un conjunto de datos sintéticos similar al que usamos para K-Means, pero esta vez los clusters no tendrán formas esféricas, lo que hará que GMM sea una opción más adecuada. El siguiente código en Python muestra cómo aplicar GMM utilizando la biblioteca scikit-learn y cómo visualizar los resultados.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.mixture import GaussianMixture
# Generar datos sintéticos con formas elípticas
np.random.seed(42)
X = np.vstack([
np.random.normal(loc=[0.0, 0.0], scale=[1.5, 0.5], size=(100, 2)),
np.random.normal(loc=[5.0, 5.0], scale=[1.0, 2.0], size=(100, 2)),
np.random.normal(loc=[10.0, 0.0], scale=[0.5, 1.5], size=(100, 2))
])
# Aplicar Gaussian Mixture Model
gmm = GaussianMixture(n_components=3, random_state=42)
gmm.fit(X)
y_gmm = gmm.predict(X)
# Visualizar los clusters
plt.scatter(X[:, 0], X[:, 1], c=y_gmm, s=50, cmap='viridis')
plt.title('Clusters generados por Gaussian Mixture Models')
plt.show()
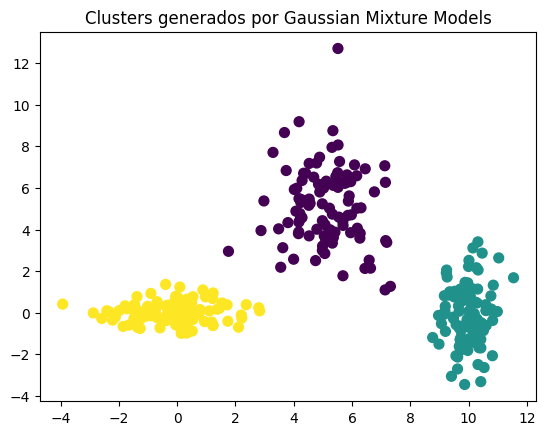
En este ejemplo, hemos generado tres clusters con formas elípticas y los hemos agrupado utilizando GMM. A diferencia de K-Means, que asume que los clusters son esféricos, GMM puede adaptarse mejor a formas más complejas, como elipses, gracias a su enfoque basado en la probabilidad. El gráfico resultante muestra cómo GMM agrupa los datos en clusters de acuerdo con la distribución de las gaussianas subyacentes.
Una de las grandes ventajas de GMM sobre K-Means es su capacidad para capturar la variabilidad dentro de los clusters, lo que lo hace más flexible en situaciones donde los datos no están bien separados en grupos definidos. Sin embargo, también es más complejo de implementar y requiere un mayor esfuerzo computacional, ya que implica calcular probabilidades y ajustar parámetros iterativamente.
¿Qué es Expectation-Maximization (EMM) y cómo mejora GMM?
El algoritmo Expectation-Maximization (EMM) es una técnica iterativa utilizada por Gaussian Mixture Models (GMM) para ajustar los parámetros de las distribuciones gaussianas que modelan los datos. EMM es esencial para que GMM pueda identificar los clusters de manera precisa, incluso en situaciones donde los clusters no son fácilmente separables.
El proceso de EMM se compone de dos pasos principales: Expectation (E) y Maximization (M). Estos pasos se repiten de manera alternada hasta que los parámetros convergen, es decir, hasta que los ajustes dejan de mejorar significativamente. A continuación, te explico en qué consiste cada uno de estos pasos:
1. Expectation (E)
En la fase de Expectation, el algoritmo calcula la probabilidad de que cada punto de datos pertenezca a cada uno de los clusters basándose en los parámetros actuales de las distribuciones gaussianas. Esta probabilidad se llama responsabilidad, y se utiliza para ponderar cómo contribuye cada punto de datos a cada cluster.
Por ejemplo, si un punto de datos está más cerca de una distribución gaussiana específica, la probabilidad de que pertenezca a ese cluster será mayor. Esto permite que un mismo punto de datos pueda pertenecer parcialmente a varios clusters, lo que es una gran ventaja de GMM sobre K-Means, que asigna cada punto de datos a un único cluster de forma determinista.
2. Maximization (M)
En la fase de Maximization, el algoritmo ajusta los parámetros de las distribuciones gaussianas (como la media, la covarianza y los pesos de los clusters) para maximizar la probabilidad total de que los datos se ajusten a estas distribuciones, utilizando las responsabilidades calculadas en la fase E. Básicamente, el algoritmo intenta encontrar la mejor configuración de las gaussianas para que representen los datos de manera más precisa.
Después de actualizar los parámetros, el proceso vuelve a la fase E para recalcular las probabilidades con los nuevos parámetros, y así sucesivamente. Este ciclo de Expectation y Maximization continúa hasta que los parámetros convergen, lo que significa que el algoritmo ha encontrado la mejor representación posible de los datos con las distribuciones gaussianas.
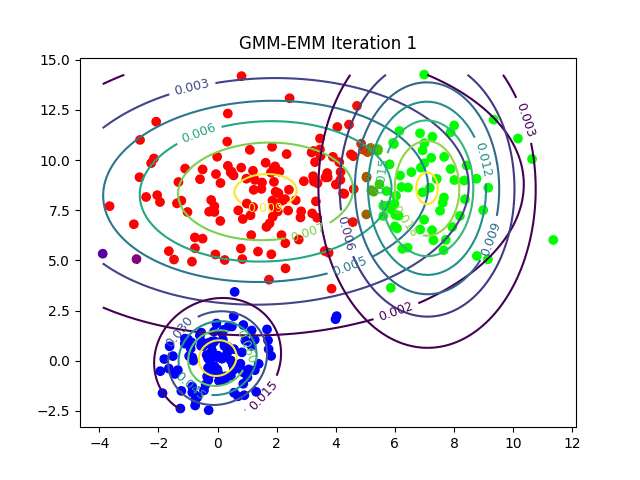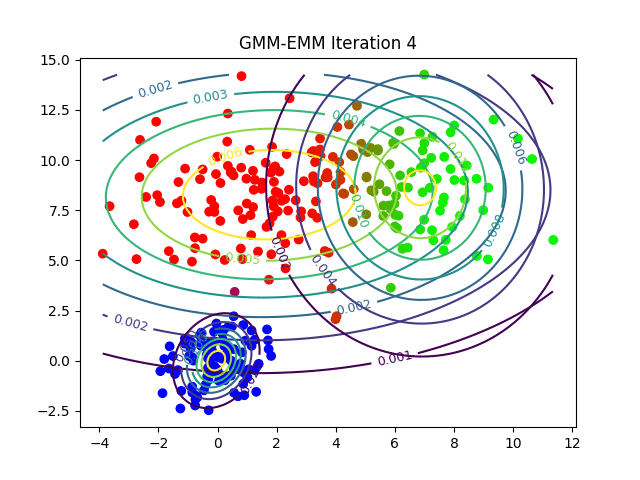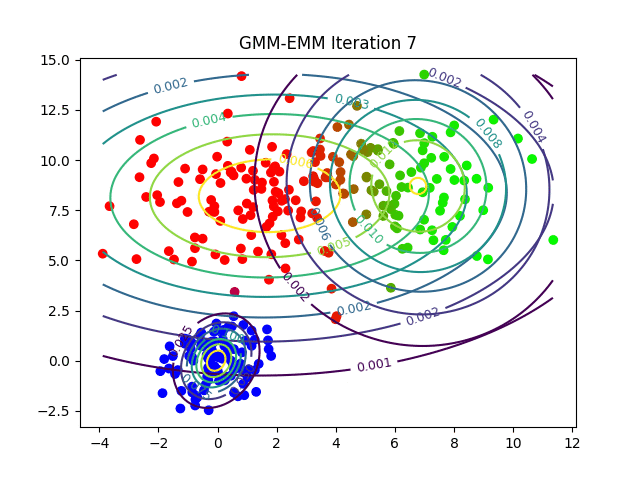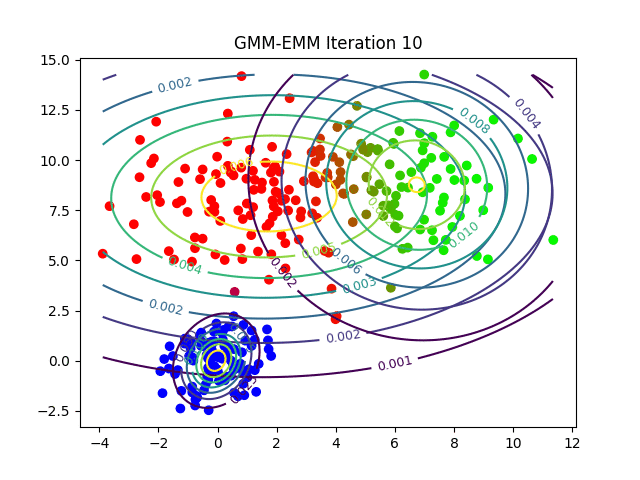
Podemos observar cómo EMM ajusta las distribuciones gaussianas para agrupar los datos de manera más efectiva. Este proceso es crucial para que GMM pueda modelar clusters complejos y no lineales, permitiendo una clasificación más precisa en comparación con K-Means.
Aunque EMM hace que GMM sea más poderoso y flexible, también lo hace más computacionalmente intensivo y más difícil de implementar en comparación con K-Means. Esto significa que, dependiendo de la complejidad de los datos y los recursos disponibles, K-Means podría ser una opción más práctica en algunos casos, mientras que GMM será más adecuado para datos que requieren un enfoque más sofisticado.
Comparación directa: K-Means vs Gaussian Mixture Models
Tanto K-Means como Gaussian Mixture Models (GMM) son algoritmos poderosos para el clustering, pero sus enfoques y aplicaciones pueden ser muy diferentes. Aquí te presentamos una comparación directa para ayudarte a decidir cuál es el más adecuado para tus necesidades específicas.
1. Método de Agrupación
K-Means: Agrupa los datos basándose en la distancia euclidiana entre los puntos y los centroides. Cada punto de datos pertenece a un solo cluster, lo que lo hace ideal para datasets donde los clusters son esféricos y de tamaño similar.
GMM: Agrupa los datos basándose en la probabilidad de que un punto pertenezca a cada cluster, utilizando una combinación de distribuciones gaussianas. Esto permite que un punto de datos pertenezca parcialmente a varios clusters, lo que es útil en situaciones donde los clusters tienen formas elípticas o no son bien definidos.
2. Flexibilidad en la Forma de los Clusters
K-Means: Supone que los clusters son esféricos y equidistantes, lo que puede limitar su efectividad en datasets con clusters de formas irregulares o de tamaños diferentes. Es menos flexible en cuanto a la forma de los clusters que puede identificar.
GMM: Puede manejar clusters con formas más complejas y elípticas gracias a la modelización basada en gaussianas. Esto lo hace más flexible y capaz de capturar la variabilidad dentro de los clusters.
3. Complejidad Computacional
K-Means: Es un algoritmo relativamente simple y rápido de implementar. Debido a su baja complejidad computacional, es adecuado para grandes datasets y situaciones donde se requiere una agrupación rápida.
GMM: Es más computacionalmente intensivo que K-Means debido al uso de Expectation-Maximization (EMM) para ajustar los parámetros. Aunque ofrece mayor precisión en situaciones complejas, también requiere más recursos y tiempo de cálculo.
4. Robustez frente a Inicializaciones
K-Means: Puede ser sensible a la inicialización de los centroides. Si los centroides iniciales no se eligen bien, K-Means podría converger a un mínimo local, lo que significa que no siempre encuentra la mejor agrupación posible.
GMM: También puede ser sensible a la inicialización, pero gracias al proceso de EMM, tiene una mayor capacidad para ajustarse a la distribución real de los datos, lo que puede mitigar parcialmente este problema.
5. Aplicaciones Comunes
K-Means: Es ampliamente utilizado en aplicaciones donde los clusters son aproximadamente esféricos y bien definidos, como en la segmentación de clientes, agrupación de documentos, y análisis de imágenes.
GMM: Se utiliza en aplicaciones donde se necesita capturar la variabilidad dentro de los clusters o cuando los datos no forman clusters esféricos, como en el modelado de distribuciones en finanzas, reconocimiento de patrones, y análisis genómico.
6. Interpretabilidad
K-Means: Es fácil de interpretar ya que cada punto de datos pertenece claramente a un único cluster. Esto lo hace más accesible para quienes buscan simplicidad en la interpretación.
GMM: Ofrece una interpretación más compleja, ya que un punto de datos puede pertenecer parcialmente a varios clusters. Aunque esto proporciona mayor flexibilidad, puede complicar la interpretación y la explicación de los resultados.
7. Robustez frente a Outliers
K-Means: Es sensible a los outliers, ya que un punto atípico puede alterar significativamente la posición de los centroides y, por lo tanto, afectar la agrupación.
GMM: También puede verse afectado por outliers, pero su enfoque probabilístico le permite manejar de manera más suave la influencia de estos puntos atípicos.
8. Elección del Número de Clusters
K-Means: Requiere que el número de clusters (K) se defina de antemano, lo que puede ser un desafío si no se conoce el número adecuado de clusters en el dataset.
GMM: También requiere la especificación del número de componentes gaussianos, pero se pueden utilizar criterios de selección como BIC (Bayesian Information Criterion) para evaluar diferentes modelos y elegir el número óptimo de componentes.
Conclusión
Tanto K-Means como Gaussian Mixture Models (GMM) son algoritmos de clustering fundamentales en el análisis de datos, pero sus enfoques y aplicaciones son muy diferentes. La elección entre uno u otro dependerá en gran medida de las características de tus datos y del objetivo específico de tu análisis.
Si estás trabajando con datos donde los clusters son aproximadamente esféricos y bien separados, K-Means puede ser una opción rápida y efectiva. Su simplicidad lo hace ideal para aplicaciones donde la interpretabilidad y la eficiencia computacional son cruciales. Sin embargo, es importante tener en cuenta sus limitaciones, especialmente en datasets donde los clusters no tienen formas regulares o donde hay outliers que podrían distorsionar los resultados.
Por otro lado, si tus datos presentan clusters con formas más complejas, como elípticas, o si necesitas un enfoque más flexible que pueda capturar la variabilidad dentro de los clusters, GMM es la herramienta adecuada. Su capacidad para modelar datos mediante una combinación de distribuciones gaussianas lo hace más robusto en situaciones donde K-Means podría fallar. No obstante, esta flexibilidad viene con un mayor costo computacional y una interpretación más compleja.
En resumen, no existe un algoritmo "mejor" de manera absoluta; la elección correcta depende del contexto. Para problemas simples y bien definidos, K-Means es una opción excelente. Pero cuando los datos son más complejos y se requiere una mayor precisión, GMM ofrece una solución más sofisticada, aunque a un mayor costo en términos de recursos y complejidad.
Finalmente, al enfrentar un problema de clustering, considera realizar pruebas con ambos algoritmos para evaluar cuál se ajusta mejor a tus datos y objetivos. Utiliza herramientas como la visualización de datos y métricas de evaluación como el BIC o silhouette score para tomar una decisión informada.
Recursos adicionales
Si te interesa profundizar en los conceptos de K-Means, Gaussian Mixture Models (GMM) y otras técnicas de clustering, aquí te dejamos algunos recursos que te serán de gran utilidad:
- Scikit-Learn Documentation: K-Means Clustering : Documentación oficial de Scikit-Learn sobre K-Means, con ejemplos y detalles técnicos.
- Scikit-Learn Documentation: Gaussian Mixture Models : Guía completa sobre GMM en Scikit-Learn, incluyendo cómo aplicar EMM y ajustar los parámetros.
- Understanding K-Means Clustering in Machine Learning : Un artículo en Towards Data Science que explica K-Means de manera visual y detallada, ideal para principiantes.
- Gaussian Mixture Models Explained : Artículo en Towards Data Science que desglosa GMM con ejemplos y visualizaciones que facilitan su comprensión.
- Machine Learning Mastery: K-Means vs. GMM : Video tutorial en YouTube que compara K-Means y GMM, con ejemplos prácticos en Python.
- Machine Learning by Stanford University (Coursera) : Curso en línea que cubre K-Means y otros algoritmos de clustering, ideal para quienes buscan una formación más formal en machine learning.
- Naive Bayes vs. Gaussian Mixture Models: Understanding the Differences : Artículo en Analytics Vidhya que compara GMM con Naive Bayes, otra técnica de clasificación probabilística.
Estos recursos te proporcionarán una comprensión más profunda y práctica de cómo funcionan K-Means y GMM, y cómo aplicarlos en tus proyectos de machine learning. ¡Explóralos y sigue aprendiendo!