Data Science

¿Qué es K-Means y para qué sirve?

Por Antonio Richaud, Publicado el 7 de Febrero de 2024

Introducción

En el ámbito del aprendizaje automático y la minería de datos, la agrupación de datos es fundamental para descubrir patrones ocultos, identificar tendencias y realizar análisis predictivos. Uno de los algoritmos más utilizados para este fin es K-Means, un método de clustering que divide un conjunto de datos en grupos o clusters basados en la similitud de sus características.

Este artículo explora en profundidad qué es el algoritmo K-Means, cómo funciona y, lo más importante, para qué sirve. A lo largo del texto, desglosaremos tanto la teoría como la implementación práctica de K-Means, ayudándote a comprender su utilidad en diversas aplicaciones y cómo puedes utilizarlo en tus propios proyectos.

¿Qué es K-Means?

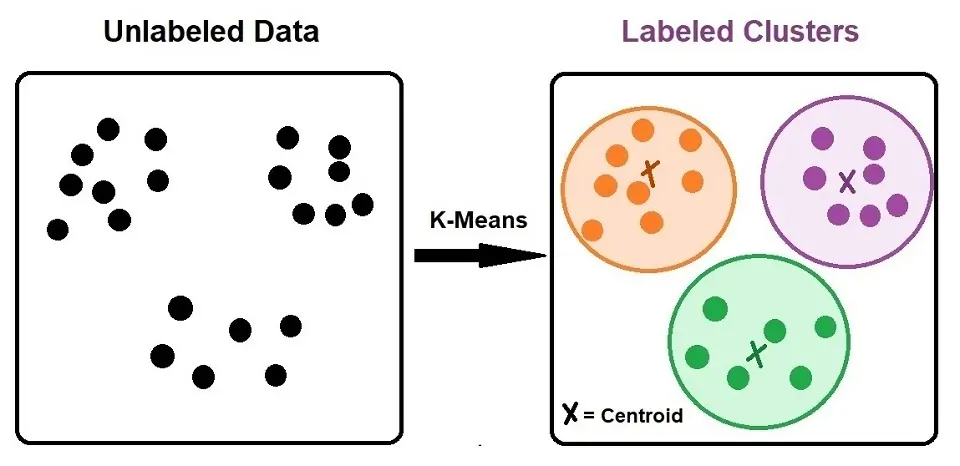
K-Means es un algoritmo de clustering o agrupamiento utilizado en aprendizaje automático para dividir un conjunto de datos en K grupos o clusters distintos. El objetivo es que los puntos de datos dentro de un mismo cluster sean lo más similares posible entre sí, y lo más diferentes posibles de los puntos en otros clusters. La similitud se mide típicamente utilizando la distancia euclidiana.

El algoritmo fue introducido por primera vez en la década de 1950, pero ha evolucionado y se ha refinado a lo largo de los años, convirtiéndose en una de las herramientas más utilizadas en análisis de datos. La simplicidad de K-Means y su capacidad para manejar grandes volúmenes de datos lo hacen ideal para una amplia variedad de aplicaciones, desde segmentación de clientes hasta compresión de imágenes.

Algunos conceptos clave en K-Means incluyen:

Cluster: Un grupo de datos que comparten características similares.
Centroide: El punto central o promedio de un cluster, que se utiliza como referencia para la agrupación de datos.
Iteración: El proceso de repetición de pasos en el algoritmo hasta que se cumplen ciertos criterios de convergencia.

¿Cómo funciona el algoritmo K-Means?

El algoritmo K-Means sigue un proceso iterativo que busca dividir un conjunto de datos en K clusters distintos. A continuación, se detallan los pasos clave del funcionamiento de K-Means:

Paso 1: Inicialización de centroides

El primer paso del algoritmo es seleccionar K puntos iniciales llamados centroides. Estos puntos pueden seleccionarse de manera aleatoria o utilizando técnicas más avanzadas como K-Means++, que intenta mejorar la inicialización para evitar malos resultados.

Paso 2: Asignación de puntos a los centroides

En este paso, cada punto de datos en el conjunto se asigna al centroide más cercano, formando así K clusters. La cercanía se mide típicamente mediante la distancia euclidiana entre el punto y el centroide.

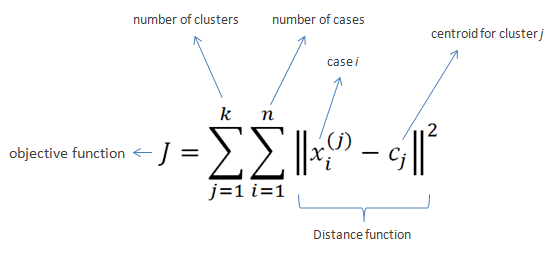
Paso 3: Recalcular centroides

Una vez que todos los puntos se han asignado a un cluster, se recalculan los centroides. Cada nuevo centroide es el promedio de todos los puntos en su cluster respectivo. Este proceso asegura que los centroides se muevan hacia las áreas de mayor densidad de datos.

Paso 4: Iteración hasta la convergencia

Los pasos 2 y 3 se repiten de forma iterativa hasta que los centroides ya no cambian significativamente, o hasta que se alcance un número máximo de iteraciones. Este estado se llama convergencia, y marca el final del proceso de clustering.

Ventajas y limitaciones de K-Means

Ventajas:

Simplicidad: fácil de entender e implementar.
Rapidez: es eficiente en términos computacionales, especialmente con grandes conjuntos de datos.

Limitaciones:

Sensibilidad a la inicialización: diferentes inicializaciones pueden conducir a diferentes resultados.
Requiere especificar el número de clusters (K) previamente, lo cual no siempre es evidente.
No maneja bien clusters de formas irregulares o de tamaños muy diferentes.

Implementación práctica de K-Means

Ahora que hemos cubierto la teoría detrás de K-Means, veamos cómo implementarlo en la práctica utilizando Python y la popular librería de aprendizaje automático Scikit-learn. En esta sección, te guiaré paso a paso a través del proceso de implementación.

Librerías y herramientas necesarias

Antes de comenzar, asegúrate de tener instaladas las siguientes librerías en tu entorno de desarrollo:

pip install numpy pandas matplotlib scikit-learn

Paso 1: Cargar y explorar los datos

Comencemos cargando un conjunto de datos y explorándolo para entender sus características. Utilizaremos el conjunto de datos iris, que es un clásico para pruebas de clustering:

import pandas as pd
from sklearn.datasets import load_iris
				
# Cargar el conjunto de datos iris
iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
				
# Visualizar las primeras filas del dataset
df.head()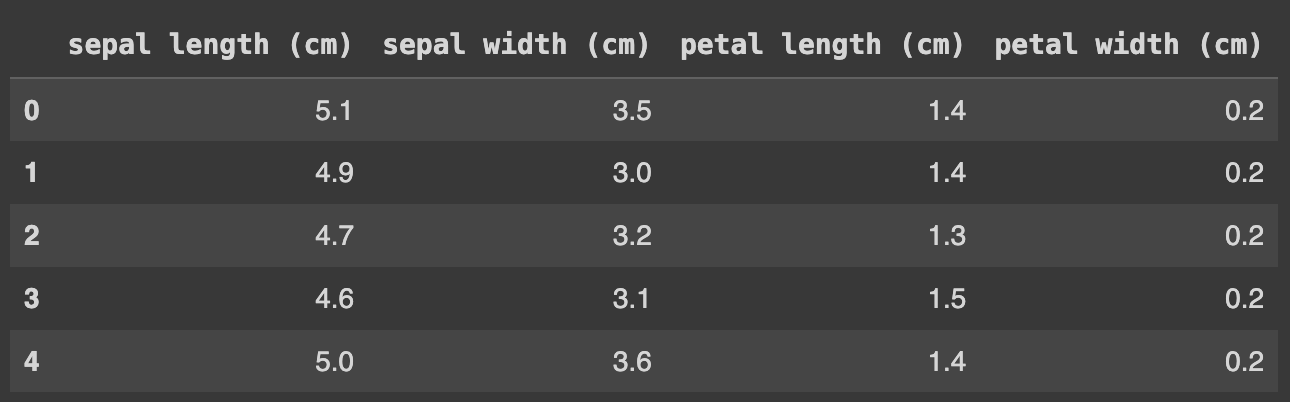

Paso 2: Seleccionar características para clustering

El siguiente paso es seleccionar las características que utilizaremos para aplicar K-Means. En este caso, utilizaremos todas las características del conjunto de datos iris:

from sklearn.preprocessing import StandardScaler
				
# Seleccionar características
X = df
				
# Estandarizar las características
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

Paso 3: Aplicar K-Means

Aplicamos el algoritmo K-Means al conjunto de datos estandarizado, especificando el número de clusters K:

from sklearn.cluster import KMeans
				
# Aplicar K-Means con K=3
kmeans = KMeans(n_clusters=3, random_state=42)
kmeans.fit(X_scaled)
				
# Obtener los clusters asignados para cada punto de datos
clusters = kmeans.labels_
df['Cluster'] = clusters
				
# Visualizar la asignación de clusters
df.head()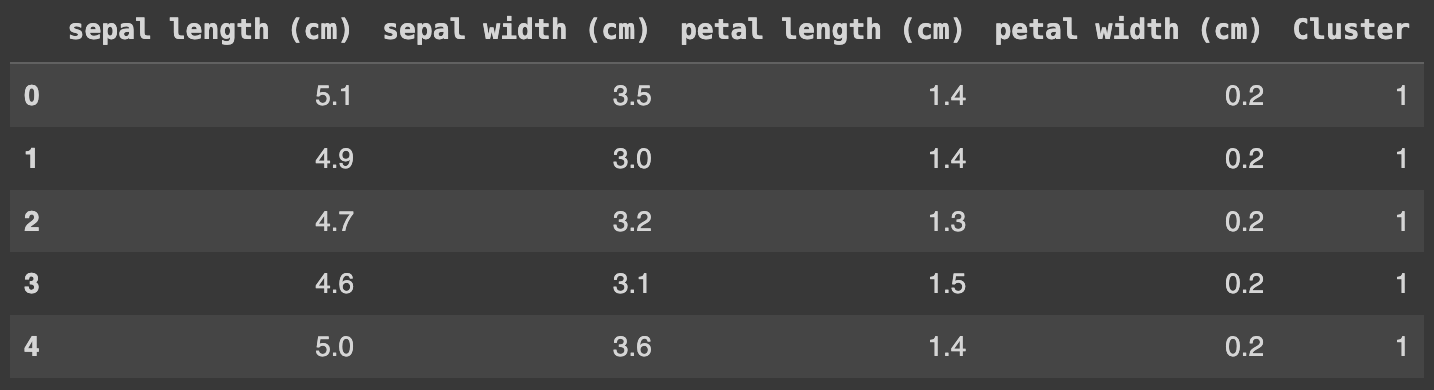

Paso 4: Visualización de resultados

Finalmente, podemos visualizar los clusters resultantes para entender mejor cómo se ha realizado la agrupación:

import matplotlib.pyplot as plt
				
# Visualizar los clusters en un scatter plot
plt.figure(figsize=(10, 6))
plt.scatter(X_scaled[:, 0], X_scaled[:, 1], c=clusters, cmap='viridis', s=100, alpha=0.7)
plt.title('Clusters resultantes del algoritmo K-Means')
plt.xlabel(iris.feature_names[0])
plt.ylabel(iris.feature_names[1])
plt.show()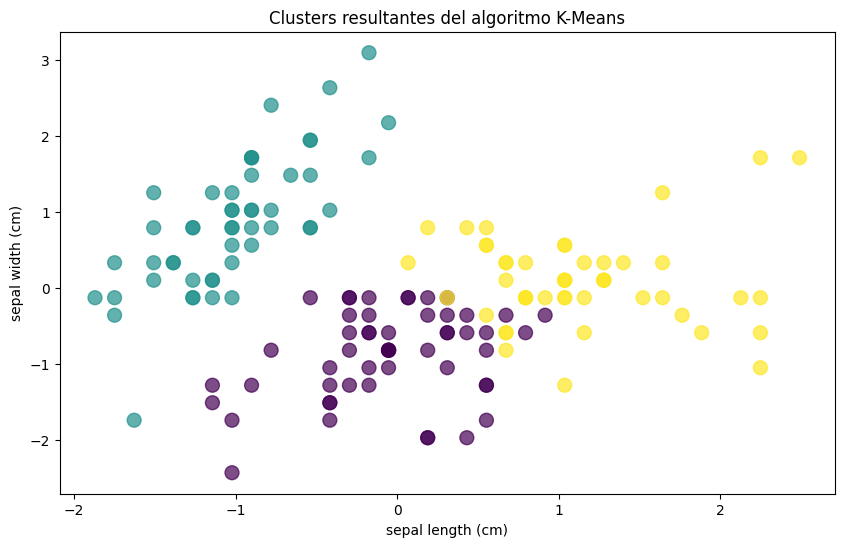

Este gráfico nos permite observar cómo K-Means ha dividido el conjunto de datos en clusters basados en las características seleccionadas.

Mejores prácticas y consejos

Para aprovechar al máximo el algoritmo K-Means, es importante seguir algunas mejores prácticas y aplicar técnicas que ayuden a optimizar y evaluar el proceso de clustering. A continuación, se presentan algunos consejos clave:

Selección del valor de K

Determinar el número adecuado de clusters (K) es uno de los mayores desafíos al utilizar K-Means. Dos métodos comunes para seleccionar K son:

Método del codo (Elbow Method): Este método implica ejecutar K-Means para diferentes valores de K y calcular la suma de los errores al cuadrado (SSE) para cada valor. Luego, se observa la gráfica del SSE frente a K y se busca un "codo" en la curva, que indica un buen equilibrio entre simplicidad y precisión.
Silhouette Analysis: Este método evalúa la cohesión interna de los clusters y su separación respecto a otros clusters. Un valor de silhouette cercano a 1 indica que los puntos están bien agrupados en su cluster y están lejos de los demás clusters.

Preprocesamiento de datos

El preprocesamiento de los datos es fundamental para el éxito de K-Means. Algunas prácticas recomendadas incluyen:

Normalización y estandarización: Dado que K-Means se basa en distancias, es crucial normalizar o estandarizar las características del conjunto de datos para evitar que las características con mayor escala dominen el proceso de clustering.
Eliminación de outliers: Los outliers pueden distorsionar los resultados del clustering, por lo que es recomendable detectarlos y, si es necesario, eliminarlos o tratarlos de manera adecuada.

Evaluación de resultados

Una vez que se ha ejecutado el algoritmo, es importante evaluar la calidad del clustering obtenido. Algunas métricas y técnicas útiles son:

SSE (Suma de los errores al cuadrado): Mide la dispersión de los puntos dentro de los clusters. Un SSE bajo indica clusters compactos.
Coeficiente de Silhouette: Como se mencionó anteriormente, esta métrica evalúa la separación entre clusters y su cohesión interna.
Visualización: Utilizar gráficos para visualizar los clusters puede proporcionar una comprensión intuitiva de cómo los datos han sido agrupados. Métodos como PCA (Análisis de Componentes Principales) pueden reducir la dimensionalidad de los datos y facilitar la visualización.

Conclusión

El algoritmo K-Means es una herramienta poderosa y versátil para el clustering de datos en el ámbito del aprendizaje automático y la minería de datos. Su simplicidad, combinada con su capacidad para manejar grandes volúmenes de datos, lo convierte en una opción popular para una amplia variedad de aplicaciones, desde la segmentación de clientes hasta la compresión de imágenes.

Sin embargo, como hemos visto, su eficacia depende en gran medida de la elección adecuada del número de clusters (K), la correcta inicialización de centroides, y el preprocesamiento adecuado de los datos. Con una implementación cuidadosa y siguiendo las mejores prácticas, K-Means puede ofrecer resultados valiosos y permitirte descubrir patrones ocultos en tus datos.

Te animo a experimentar con K-Means en tus propios proyectos y explorar cómo puede ayudarte a desentrañar la estructura subyacente de tus datos.