¿Qué es PCA, cómo funciona y cómo saber cuándo aplicarlo?
Por Antonio Richaud, Publicado el 15 de Mayo de 2024
Imagina que tienes un montón de datos en tus manos, toneladas de columnas con información sobre clientes, productos, transacciones, o incluso el desempeño de maquinaria en una planta de producción. La pregunta es, ¿cómo puedes sacarles el máximo provecho sin volverte loco intentando procesar cada detalle? Aquí es donde entra en juego el Análisis de Componentes Principales, o mejor conocido como PCA por sus siglas en inglés.
El PCA es una técnica estadística que se utiliza para reducir la dimensionalidad de un conjunto de datos, lo que significa que te ayuda a simplificar la información sin perder lo esencial. Básicamente, toma tus datos complejos y los comprime en unas pocas dimensiones que capturan la mayor parte de la variabilidad presente en el conjunto original. Así, puedes visualizar y analizar tus datos de manera más eficiente, lo que es especialmente útil cuando trabajas con grandes volúmenes de información.
Aunque el concepto de "reducción de dimensionalidad" puede sonar técnico y complicado, el PCA se ha convertido en una herramienta clave en áreas como las finanzas, el marketing, la producción y muchas otras, donde el análisis de datos juega un papel crucial en la toma de decisiones. Desde identificar patrones ocultos hasta mejorar modelos predictivos, PCA te permite enfocarte en lo que realmente importa, dejando fuera el ruido.
En este artículo, vamos a explorar qué es exactamente el PCA, cómo funciona, y lo más importante, cuándo deberías considerarlo en tus análisis de datos. Para que sea más claro y práctico, también veremos un ejemplo aplicado a un conjunto de datos financieros, de modo que puedas ver el PCA en acción y entender cómo puede ser una herramienta valiosa en el día a día de tu empresa.
¿Cómo funciona PCA?
Ahora que ya sabes qué es PCA, vamos a desglosar cómo funciona realmente. Aunque suena como un concepto complejo, la idea básica detrás del Análisis de Componentes Principales es bastante intuitiva: se trata de encontrar la manera más eficiente de representar tus datos, comprimiendo toda la información en unas pocas dimensiones sin perder lo más importante.
Entendiendo la variabilidad
Imagina que tienes un conjunto de datos con muchas variables, como las características financieras de varios clientes: ingresos, deudas, puntaje crediticio, etc. Cada una de estas variables aporta cierta cantidad de información al conjunto de datos, y juntas forman un espacio multidimensional que puede ser difícil de visualizar o analizar. Aquí es donde entra el concepto de variabilidad.
La variabilidad mide cuánto difieren los datos entre sí. Si todas las variables en tu conjunto de datos fueran exactamente iguales para todos los clientes, no habría variabilidad, y realmente no necesitarías mucho análisis. Pero en la vida real, los datos varían bastante, y PCA se enfoca en identificar qué direcciones (o componentes principales) en el espacio de datos capturan la mayor cantidad de esa variabilidad.
Los componentes principales
Los componentes principales son, básicamente, nuevas variables que PCA crea al combinar tus variables originales de una manera muy específica. La primera componente principal es la dirección en la que los datos varían más. La segunda componente principal es ortogonal a la primera (es decir, está en una dirección completamente diferente) y captura la siguiente mayor variabilidad, y así sucesivamente.
Un punto clave aquí es que estos componentes principales son lineales, es decir, son combinaciones lineales de tus variables originales. Esto significa que cada componente principal se calcula tomando una suma ponderada de tus variables originales, donde los pesos se eligen para maximizar la variabilidad capturada.
Visualización de PCA
Para visualizarlo, imagina un gráfico 3D con tres variables en los ejes X, Y y Z. Los datos de tus clientes están distribuidos en este espacio tridimensional. PCA "gira" este espacio para encontrar las direcciones (componentes) donde la distribución de los datos es más amplia. Luego, "proyecta" los datos en estas direcciones, permitiéndote reducir las tres dimensiones originales a solo dos, por ejemplo, sin perder demasiada información.
El resultado es que, en lugar de trabajar con tres variables, puedes trabajar con dos componentes principales que capturan la mayoría de la información de las tres variables originales. Esto no solo simplifica el análisis, sino que también puede hacer que tus modelos sean más eficientes y menos propensos a sobreajustarse.
Matemáticas detrás de PCA (explicadas de forma sencilla)
Si te gustan los números, aquí va una pequeña dosis de matemáticas. PCA se basa en la descomposición en valores propios (Eigenvalue Decomposition) o en la descomposición en valores singulares (Singular Value Decomposition, SVD). Sin entrar en detalles demasiado técnicos, la idea es que estas técnicas permiten descomponer la matriz de datos en vectores y valores que nos dicen en qué dirección varían más los datos y cuánta variabilidad hay en cada dirección.
Los vectores propios (eigenvectors) indican las direcciones de los componentes principales, y los valores propios (eigenvalues) indican cuánta variabilidad captura cada componente. En otras palabras, los valores propios nos dicen qué tan importantes son las diferentes direcciones identificadas por los vectores propios.
Al final del día, lo que hace PCA es calcular estos vectores y valores, ordenar los componentes principales por la cantidad de variabilidad que capturan, y luego permitirte seleccionar los componentes más importantes para tu análisis.
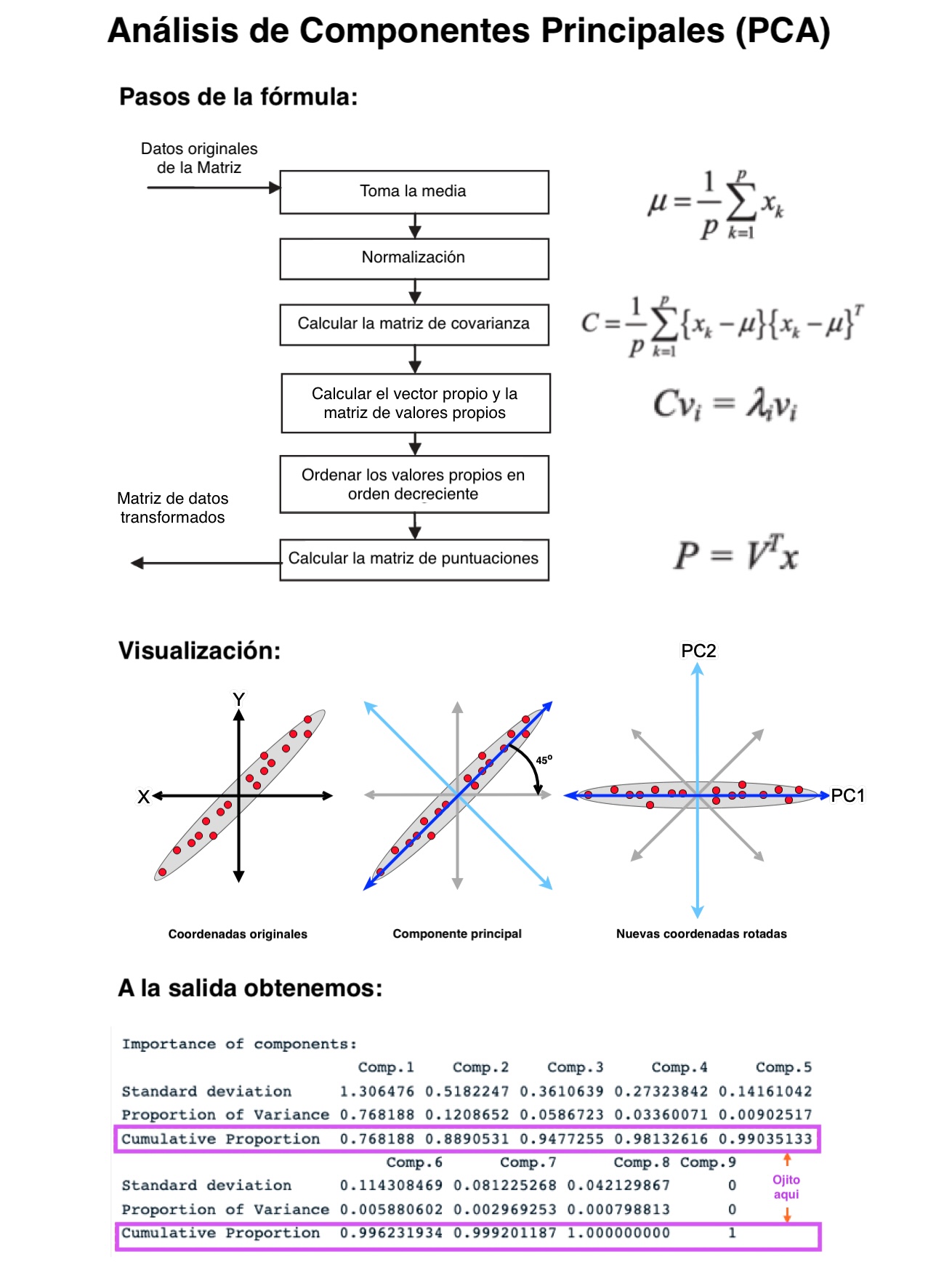
La imagen de arriba ilustra perfectamente el proceso que acabamos de explicar. Desde la toma de la media y la normalización, hasta el cálculo de la matriz de covarianza y los vectores propios, cada paso es clave para transformar los datos originales en componentes principales que capturan la mayor variabilidad posible. La visualización muestra cómo los datos originales se rotan y proyectan en un nuevo espacio donde las nuevas coordenadas, o componentes principales, representan de manera más eficiente la variabilidad de los datos.
Al final del proceso, obtendrás una tabla de importancia de componentes, donde podrás ver cuánta variabilidad captura cada componente y decidir cuántos componentes necesitas para tu análisis. Esto te ayudará a simplificar tu modelo sin perder información crítica.
¿Cuándo aplicar PCA?
Ya hemos visto qué es el PCA y cómo funciona, pero la gran pregunta es: ¿cuándo deberías usarlo? No todos los conjuntos de datos o problemas requieren una reducción de dimensionalidad, así que es crucial saber cuándo PCA puede realmente hacer una diferencia en tu análisis.
1. Cuando tienes muchas variables y sospechas que hay redundancia
Si estás trabajando con un conjunto de datos con muchas variables (columnas) y algunas de ellas parecen estar relacionadas entre sí, PCA puede ser una excelente opción. Por ejemplo, en un análisis financiero, variables como el ingreso mensual y el gasto mensual pueden estar altamente correlacionadas. En lugar de trabajar con ambas variables, PCA puede combinarlas en un solo componente principal que capture la mayor parte de la información de ambas, simplificando así tu modelo y evitando problemas de multicolinealidad.
2. Cuando quieres visualizar datos en alta dimensión
Visualizar datos en más de tres dimensiones es casi imposible, pero PCA puede ayudarte a proyectar esos datos en 2D o 3D, haciendo que sean mucho más fáciles de interpretar. Si estás analizando datos con 10, 20 o incluso más variables, PCA te permite reducir esos datos a solo dos o tres componentes principales que puedes graficar y visualizar, lo que es útil para identificar patrones, clústeres, o anomalías en los datos.
3. Cuando estás preparando datos para un modelo de Machine Learning
En Machine Learning, más no siempre es mejor. Demasiadas variables pueden hacer que un modelo sea más complejo y menos eficiente, y puede aumentar el riesgo de sobreajuste. PCA ayuda a reducir el número de variables, conservando solo aquellas que son realmente necesarias para el modelo, lo que no solo mejora la eficiencia sino que también puede aumentar la precisión del modelo al eliminar el "ruido".
4. Cuando necesitas acelerar el procesamiento de datos
Si estás trabajando con grandes volúmenes de datos y el procesamiento se está volviendo lento, reducir la dimensionalidad con PCA puede ser la solución. Al reducir el número de variables, PCA disminuye la carga computacional, lo que permite un procesamiento más rápido sin perder demasiada información. Esto es especialmente útil en entornos empresariales donde el tiempo es dinero, y se necesita analizar datos rápidamente para tomar decisiones informadas.
5. Cuando necesitas combatir la multicolinealidad
La multicolinealidad ocurre cuando dos o más variables en un conjunto de datos están altamente correlacionadas, lo que puede causar problemas en modelos de regresión o Machine Learning. PCA es una excelente herramienta para reducir la multicolinealidad, ya que combina las variables correlacionadas en componentes principales, eliminando la redundancia y haciendo que los modelos sean más robustos y precisos.
Ventajas de aplicar PCA
- Simplificación: Reduce la complejidad de los datos al condensar la información en menos variables.
- Visualización: Facilita la visualización de datos en alta dimensión.
- Eficiencia: Mejora la eficiencia computacional y la velocidad de procesamiento de modelos.
- Robustez: Ayuda a combatir la multicolinealidad y a mejorar la robustez de los modelos.
Desventajas de aplicar PCA
- Pérdida de interpretabilidad: Los componentes principales son combinaciones lineales de las variables originales, lo que puede hacer que pierdas la intuición sobre lo que representan esas nuevas variables.
- Dependencia de la escala: Si las variables no están bien escaladas, PCA puede dar resultados engañosos. Normalizar los datos antes de aplicar PCA es crucial.
- Información perdida: Aunque PCA conserva la mayor parte de la variabilidad, siempre se pierde algo de información al reducir las dimensiones.
En resumen, PCA es una herramienta poderosa, pero como toda herramienta, debe ser utilizada en el contexto adecuado. Si te encuentras en una situación donde hay demasiadas variables, quieres mejorar la eficiencia de un modelo, o necesitas visualizar datos complejos, PCA puede ser la solución que estás buscando.
Ejemplo práctico: Aplicando PCA al German Credit Data
Para poner en práctica lo que hemos aprendido, vamos a aplicar PCA a un conjunto de datos financieros. En este caso, utilizaremos el dataset "German Credit Data" disponible en Kaggle. Este dataset contiene información sobre diferentes características crediticias de individuos, como la duración del crédito, propósito, estado de cuenta, y más.
Paso 1: Cargar y explorar los datos
Primero, necesitamos cargar nuestro conjunto de datos y realizar una exploración inicial para entender su estructura. Aquí tienes un código en Python para hacerlo usando pandas:
import pandas as pd
# Cargar el conjunto de datos (Descargado de Kaggle)
df = pd.read_csv('ruta/al/archivo/german_credit_data.csv')
# Mostrar las primeras filas del conjunto de datos
print(df.head())
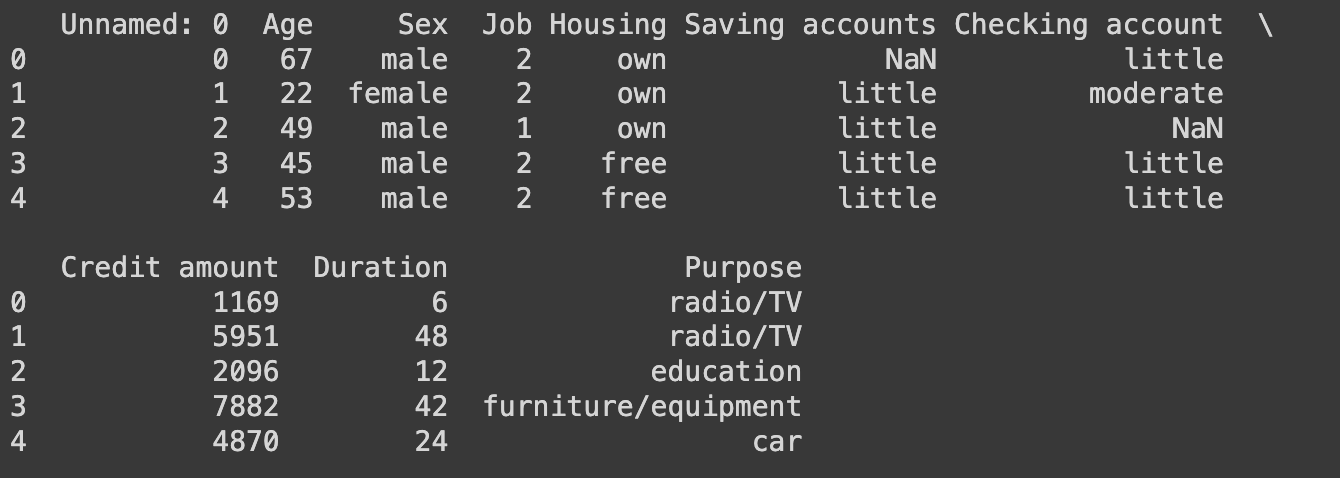
Este código carga el dataset descargado de Kaggle y muestra las primeras filas para que podamos ver cómo están estructurados los datos. Es importante familiarizarse con las variables que vamos a analizar.
Paso 2: Preprocesamiento de los datos
Antes de aplicar PCA, necesitamos preparar nuestros datos. Esto incluye manejar los valores faltantes, normalizar los datos y convertir cualquier variable categórica en numérica (aunque en este dataset, la mayoría de las variables ya son numéricas). Aquí está el código para hacerlo:
from sklearn.preprocessing import StandardScaler
# Manejo de valores faltantes en columnas numéricas
numeric_columns = df.select_dtypes(include=['number']).columns
df[numeric_columns] = df[numeric_columns].fillna(df[numeric_columns].mean())
# Normalización de los datos (solo columnas numéricas)
scaler = StandardScaler()
df_scaled = scaler.fit_transform(df[numeric_columns])
# Convertir el resultado en un DataFrame usando las columnas numéricas
df_scaled = pd.DataFrame(df_scaled, columns=numeric_columns)
print(df_scaled.head())
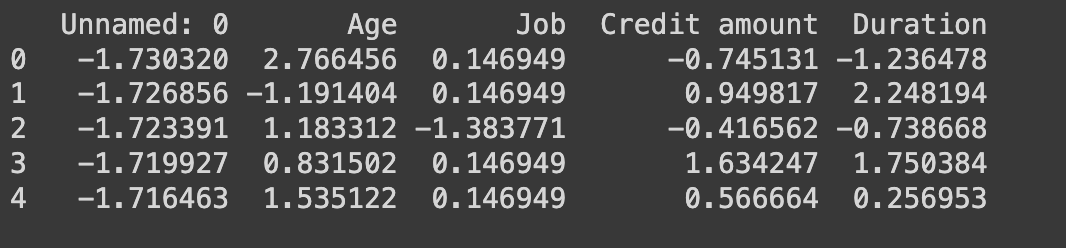
En este paso, rellenamos los valores faltantes con la media de cada columna y normalizamos los datos para que todas las variables tengan la misma escala. Esto es crucial para PCA, ya que las variables en diferentes escalas pueden sesgar los resultados.
Paso 3: Aplicar PCA
Ahora estamos listos para aplicar PCA. Vamos a reducir el número de dimensiones del dataset y ver cuántos componentes principales necesitamos para capturar la mayor parte de la variabilidad de los datos.
from sklearn.decomposition import PCA
# Aplicar PCA
pca = PCA(n_components=2) # Intentemos reducir a 2 componentes principales
df_pca = pca.fit_transform(df_scaled)
# Convertir el resultado en un DataFrame para mejor interpretación
df_pca = pd.DataFrame(df_pca, columns=['PC1', 'PC2'])
print(df_pca.head())
# Ver la cantidad de variabilidad capturada por cada componente
print('proporción de varianza explicada:', pca.explained_variance_ratio_)
print('Suma de la varianza explicada:', sum(pca.explained_variance_ratio_))
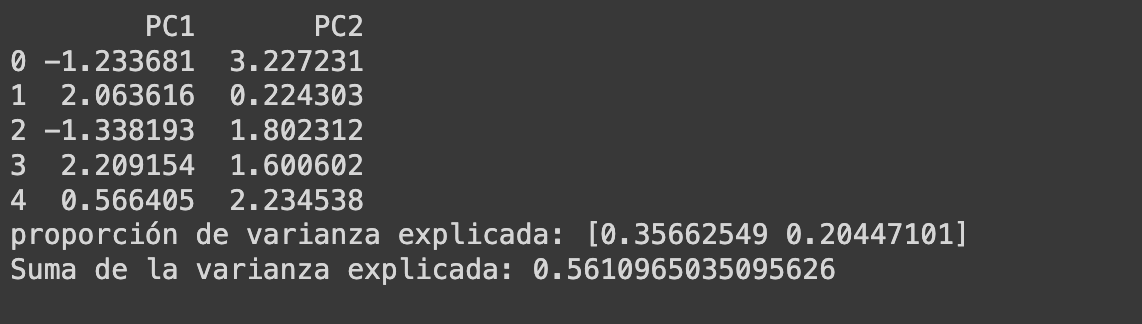
En este código, aplicamos PCA y reducimos nuestro dataset a solo 2 componentes principales. También mostramos cuánta variabilidad captura cada componente, lo que nos ayuda a decidir si 2 componentes son suficientes o si necesitamos más para mantener la mayor parte de la información.
Paso 4: Visualizar los resultados
La visualización es una parte clave del análisis de PCA. Vamos a graficar los dos primeros componentes principales para ver cómo se distribuyen los datos en este nuevo espacio reducido.
import matplotlib.pyplot as plt
# Graficar los dos primeros componentes principales
plt.figure(figsize=(10, 6))
plt.scatter(df_pca['PC1'], df_pca['PC2'], c='blue', edgecolor='k', s=50)
plt.title('Distribución de clientes en el espacio de los primeros dos componentes principales')
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.grid(True)
plt.show()
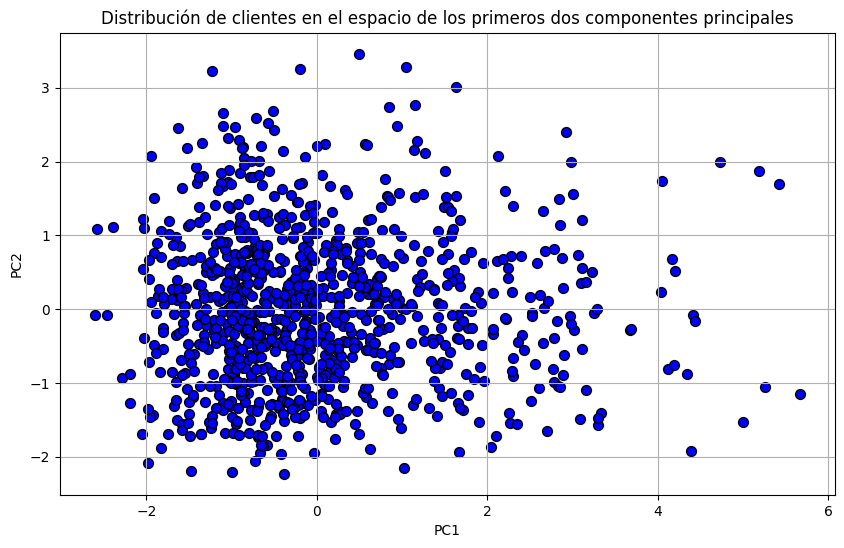
Esta gráfica muestra cómo los datos se agrupan en el espacio de los primeros dos componentes principales. Si vemos patrones claros, como clústeres o tendencias, esto indica que PCA ha capturado bien la variabilidad de los datos, y podemos usar estos componentes para análisis adicionales o como input para un modelo de Machine Learning.
Interpretación de los resultados
Después de aplicar PCA, la interpretación de los resultados es crucial. En nuestro ejemplo, hemos reducido el dataset a 2 componentes principales que explican la mayor parte de la variabilidad. Esto significa que, en lugar de analizar todas las variables originales, podemos centrarnos en estos dos componentes, lo que simplifica enormemente el análisis sin sacrificar demasiada información.
Por ejemplo, si los clientes se agrupan en diferentes áreas del gráfico, podríamos interpretar estos grupos como diferentes segmentos de riesgo crediticio. También podemos utilizar los componentes principales como variables en modelos predictivos, lo que puede mejorar la eficiencia y la precisión del modelo al reducir el "ruido" de las variables originales.
Al final, el objetivo de PCA es simplificar tu trabajo con datos manteniendo la esencia de la información. Al aplicar PCA correctamente, puedes transformar un conjunto de datos complejo en algo mucho más manejable y fácil de interpretar, permitiéndote tomar decisiones más informadas y eficaces.
Conclusión
El Análisis de Componentes Principales (PCA) es una herramienta poderosa para simplificar el análisis de datos al reducir la dimensionalidad de los conjuntos de datos sin perder información clave. En el contexto de las finanzas y otros campos empresariales, PCA puede ser particularmente útil para identificar patrones, reducir la multicolinealidad y mejorar la eficiencia de los modelos predictivos.
A lo largo de este artículo, hemos explorado qué es PCA, cómo funciona, cuándo aplicarlo, y cómo utilizarlo en un caso práctico utilizando un conjunto de datos financieros. El ejemplo práctico demostró cómo PCA puede condensar un gran número de variables en unas pocas componentes principales, lo que facilita la interpretación de los datos y la toma de decisiones.
Aunque PCA es una técnica valiosa, es importante recordar que no es la solución adecuada para todos los problemas de análisis de datos. Como cualquier herramienta, debe aplicarse con cuidado, considerando tanto sus ventajas como sus limitaciones. Si se utiliza correctamente, PCA puede transformar datos complejos en información procesable, optimizando tanto la eficiencia como la precisión de los modelos y análisis.
Te invito a que experimentes con PCA en tus propios conjuntos de datos y veas cómo puede ayudarte a simplificar y mejorar tus análisis. Con la práctica, PCA puede convertirse en una parte integral de tu conjunto de herramientas de análisis de datos.
Recursos adicionales
Si quieres profundizar más en el uso de PCA y otras técnicas de análisis de datos, aquí tienes algunos recursos útiles:
- German Credit Data en Kaggle: El dataset utilizado en este ejemplo, ideal para practicar PCA en un contexto financiero.
- Documentación de PCA en scikit-learn: Una guía completa para implementar PCA en Python utilizando la popular biblioteca scikit-learn.
- Practical Guide to PCA in Python: Un tutorial detallado sobre cómo aplicar PCA en Python con ejemplos y visualizaciones.
- Machine Learning Course by Andrew Ng: Un curso introductorio que cubre muchos conceptos de Machine Learning, incluido PCA.
- Libro: Data Science from Scratch: Un excelente recurso para aprender los fundamentos de la ciencia de datos y técnicas como PCA desde cero.
Estos recursos proporcionan una base sólida para continuar aprendiendo y aplicando PCA en diferentes contextos, mejorando tus habilidades en análisis de datos y Machine Learning.