
¿Qué es y para qué sirve el algoritmo Dijkstra?
Por Antonio Richaud, Publicado el 20 de Marzo de 2024
Introducción
Algoritmos hay muchos, pero pocos son tan importantes y útiles como el algoritmo de Dijkstra. Si alguna vez has usado Google Maps para encontrar la ruta más rápida a tu destino, has aprovechado los conceptos detrás de este algoritmo, aunque no lo supieras. Dijkstra es una de esas herramientas matemáticas que, aunque parezca complicada al principio, tiene aplicaciones súper prácticas en la vida cotidiana.
En este artículo, te voy a explicar de manera sencilla qué es el algoritmo de Dijkstra, cómo funciona y, lo más importante, para qué se utiliza. Ya sea que estés interesado en la informática, la ingeniería, o simplemente tengas curiosidad por saber cómo los sistemas encuentran la ruta más corta entre dos puntos, este artículo es para ti. Vamos a desmenuzar el algoritmo paso a paso, con ejemplos claros y fáciles de entender.
1. ¿Qué es el algoritmo de Dijkstra?
El algoritmo de Dijkstra es una técnica utilizada en informática y matemáticas para encontrar el camino más corto entre dos puntos en un grafo. Un grafo es una estructura que se usa para representar conexiones entre diferentes elementos, llamados "nodos" o "vértices". Por ejemplo, un grafo podría representar un mapa de una ciudad, donde cada nodo es una intersección y cada conexión entre nodos es una calle.
Contexto histórico: ¿Quién fue Dijkstra?
El algoritmo lleva el nombre de Edsger W. Dijkstra, un científico de la computación de los Países Bajos que lo desarrolló en 1956. Dijkstra es uno de los pioneros de la informática moderna, y su algoritmo es uno de los más conocidos y utilizados en el campo de las ciencias de la computación. Lo increíble es que Dijkstra creó este algoritmo en un momento en que las computadoras eran mucho menos potentes que hoy, lo que demuestra su brillantez al diseñar soluciones eficientes y elegantes.
Grafos y el algoritmo de Dijkstra
Como mencioné antes, un grafo es una estructura compuesta por nodos (que representan puntos) y aristas (que representan las conexiones entre esos puntos). El algoritmo de Dijkstra trabaja sobre grafos ponderados, es decir, grafos donde cada conexión entre nodos tiene un "peso" o "costo" asociado. Este peso podría ser la distancia entre dos lugares, el tiempo que tarda en recorrer un tramo, o cualquier otra medida que quieras optimizar.
El objetivo del algoritmo de Dijkstra es encontrar el camino más corto desde un nodo inicial hasta un nodo destino, minimizando el costo total del viaje. Esto se logra recorriendo el grafo y eligiendo en cada paso la conexión más barata disponible, hasta llegar al destino.
Aquí te dejo un ejemplo visual básico de un grafo, para que entiendas mejor cómo funciona:
A---1---B
| |
4| |3
| |
C---2---D
En este grafo, cada letra representa un nodo y cada número representa el "costo" de moverse entre esos nodos. Por ejemplo, moverse de A a B cuesta 1, mientras que de A a C cuesta 4.
2. ¿Para qué sirve el algoritmo de Dijkstra?
El algoritmo de Dijkstra se utiliza principalmente para encontrar el camino más corto entre dos puntos en un grafo, minimizando el costo total del recorrido. Este tipo de problema es común en muchas aplicaciones de la vida real, especialmente en áreas como la navegación, las redes de telecomunicaciones, y el diseño de rutas en logística. A continuación, te presento algunas de las aplicaciones más comunes del algoritmo de Dijkstra.
Navegación y mapas
Una de las aplicaciones más evidentes del algoritmo de Dijkstra es en los sistemas de navegación. Imagina que estás usando una aplicación de mapas como Google Maps para encontrar la ruta más rápida desde tu casa hasta tu trabajo. Lo que hace el algoritmo es evaluar todas las rutas posibles entre ambos puntos y seleccionar la que tiene el menor costo, que en este caso sería el tiempo de viaje o la distancia más corta. Gracias a Dijkstra, estos sistemas pueden proporcionarte una ruta optimizada en cuestión de segundos.
Redes de comunicación
En el ámbito de las telecomunicaciones, el algoritmo de Dijkstra se utiliza para encontrar el camino más eficiente para enviar datos a través de una red. Cada nodo en la red puede representar un enrutador o un servidor, y las conexiones entre ellos pueden tener diferentes costos en función de la latencia, el ancho de banda disponible o la congestión del tráfico. Al utilizar el algoritmo de Dijkstra, los proveedores de servicios pueden garantizar que los datos viajen por la ruta más rápida y eficiente posible.
Planificación de rutas y logística
Las empresas de logística y transporte también usan este algoritmo para optimizar las rutas de entrega. Por ejemplo, si una empresa tiene que entregar paquetes en varias ubicaciones, el algoritmo de Dijkstra puede ayudar a planificar la ruta más corta, reduciendo así los costos de transporte y el tiempo de entrega.
Problemas de camino más corto en la vida real
Además de las aplicaciones mencionadas, el algoritmo de Dijkstra se utiliza en cualquier problema donde necesites encontrar el camino más corto entre dos puntos. Esto incluye desde videojuegos, donde los personajes necesitan encontrar la mejor ruta para llegar a su objetivo, hasta la planificación de redes eléctricas, donde es crucial minimizar las pérdidas de energía.
3. ¿Cómo funciona el algoritmo de Dijkstra?
El algoritmo de Dijkstra es un proceso sistemático para encontrar el camino más corto desde un nodo inicial hasta todos los otros nodos en un grafo. A continuación, te explico paso a paso cómo funciona este algoritmo utilizando un ejemplo sencillo y las imágenes que compartiste para que lo veas de manera visual.
Paso 1: Inicialización
Primero, inicializamos todos los nodos con una distancia "infinita" (∞) excepto el nodo inicial, que se establece en 0 porque la distancia desde el nodo inicial hasta sí mismo es 0. También marcamos todos los nodos como no visitados.
Visualización inicial:
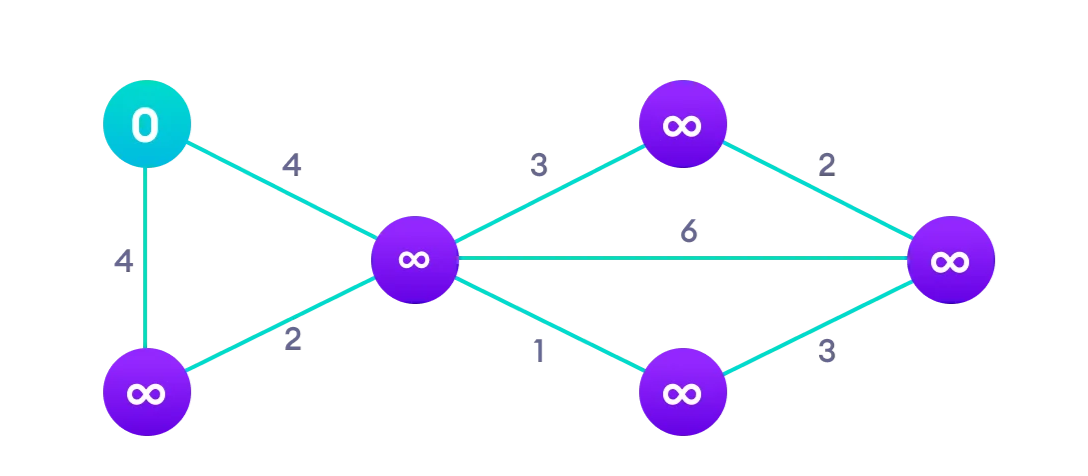
Paso 2: Evaluación de vecinos
A continuación, seleccionamos el nodo no visitado con la distancia más pequeña (en este caso, el nodo inicial) y evaluamos sus nodos vecinos. Calculamos la distancia desde el nodo inicial a cada vecino, sumando la distancia del nodo actual con el peso de la conexión a cada vecino. Si esta nueva distancia es menor que la distancia actualmente registrada para el vecino, la actualizamos.
Evaluación del primer nodo:
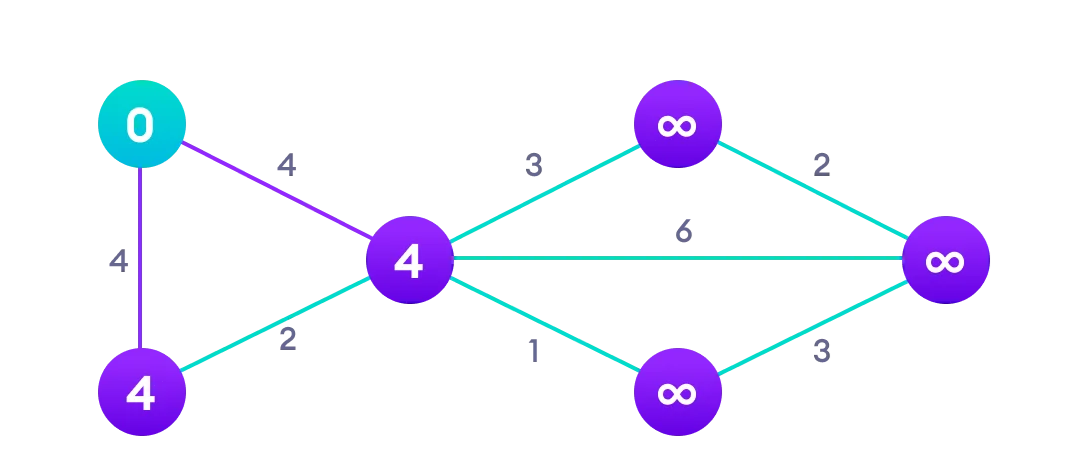
Paso 3: Marcar como visitado
Después de evaluar y actualizar las distancias de los vecinos, marcamos el nodo actual como "visitado". Esto significa que hemos encontrado la distancia más corta posible a este nodo, y ya no necesitamos reevaluarlo.
Continuación del proceso:
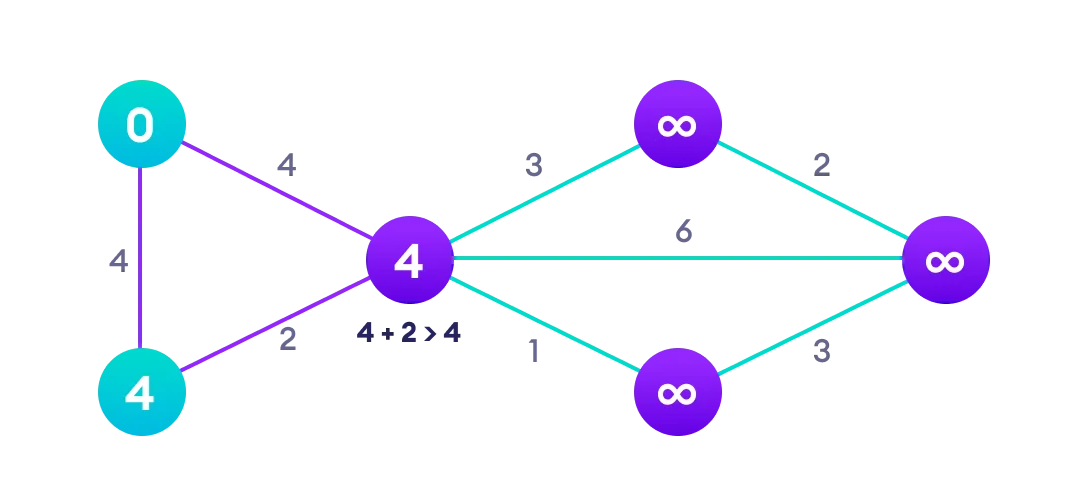
Paso 4: Repetir hasta completar
Repetimos los pasos 2 y 3 hasta que todos los nodos hayan sido visitados. Cada vez seleccionamos el nodo no visitado con la distancia más pequeña y actualizamos las distancias de sus vecinos si encontramos un camino más corto.
Resultado final:
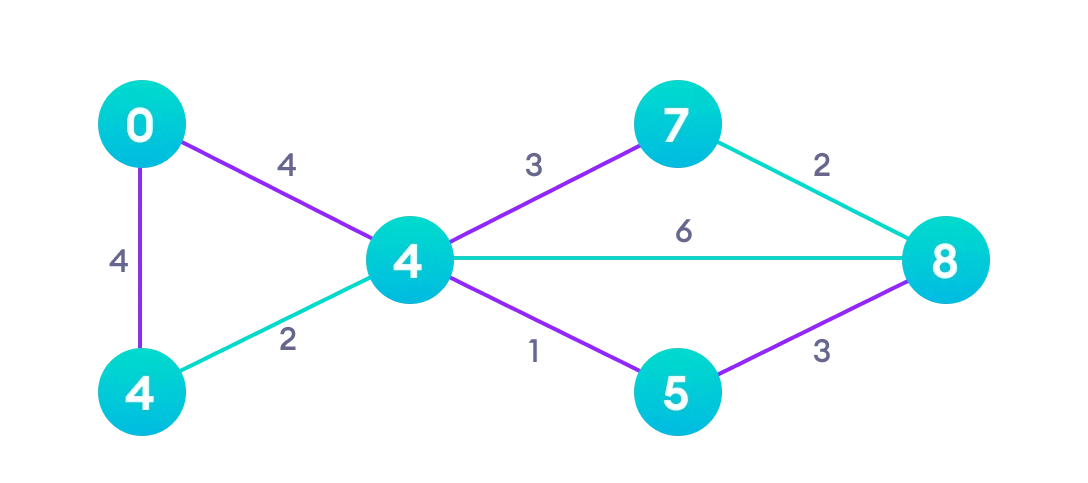
Ejemplo en pseudocódigo
Aquí te dejo un ejemplo en pseudocódigo para que entiendas mejor cómo funciona el algoritmo:
function Dijkstra(Grafo, NodoInicio):
Distancia[NodoInicio] = 0
Para cada nodo en Grafo:
si nodo != NodoInicio:
Distancia[nodo] = ∞
Anterior[nodo] = indefinido
ColaDeNodos = Grafo.Nodos
mientras ColaDeNodos no esté vacía:
NodoActual = Nodo con la menor Distancia en ColaDeNodos
ColaDeNodos.eliminar(NodoActual)
para cada vecino de NodoActual:
Ruta = Distancia[NodoActual] + DistanciaAlVecino
si Ruta < Distancia[Vecino]:
Distancia[Vecino] = Ruta
Anterior[Vecino] = NodoActual
retornar Distancia, Anterior
Este pseudocódigo muestra cómo el algoritmo de Dijkstra recorre cada nodo, actualizando las distancias más cortas desde el nodo inicial a todos los demás nodos del grafo.
Implementación en Python
Python es uno de los lenguajes más utilizados para enseñar y aplicar algoritmos debido a su simplicidad y legibilidad. Aquí te dejo un ejemplo de cómo implementar el algoritmo de Dijkstra en Python.
import heapq
def dijkstra(grafo, inicio):
distancias = {nodo: float('inf') for nodo in grafo}
distancias[inicio] = 0
cola_prioridad = [(0, inicio)]
camino = {}
while cola_prioridad:
distancia_actual, nodo_actual = heapq.heappop(cola_prioridad)
if distancia_actual > distancias[nodo_actual]:
continue
for vecino, peso in grafo[nodo_actual].items():
distancia = distancia_actual + peso
if distancia < distancias[vecino]:
distancias[vecino] = distancia
camino[vecino] = nodo_actual
heapq.heappush(cola_prioridad, (distancia, vecino))
return distancias, camino
# Ejemplo de uso
grafo = {
'A': {'B': 4, 'C': 2},
'B': {'A': 4, 'D': 3, 'E': 2},
'C': {'A': 2, 'D': 4},
'D': {'B': 3, 'C': 4, 'E': 3},
'E': {'B': 2, 'D': 3}
}
distancias, camino = dijkstra(grafo, 'A')
print("Distancias desde A:", distancias)
print("Camino más corto:", camino)
Implementación en JavaScript
JavaScript es otro lenguaje muy popular, especialmente en aplicaciones web. A continuación, te muestro cómo podrías implementar el algoritmo de Dijkstra en JavaScript.
function dijkstra(grafo, inicio) {
let distancias = {};
let visitados = {};
let cola = new MinPriorityQueue();
for (let nodo in grafo) {
distancias[nodo] = Infinity;
}
distancias[inicio] = 0;
cola.enqueue(inicio, 0);
while (!cola.isEmpty()) {
let { element: nodoActual } = cola.dequeue();
if (!visitados[nodoActual]) {
visitados[nodoActual] = true;
for (let vecino in grafo[nodoActual]) {
let distancia = distancias[nodoActual] + grafo[nodoActual][vecino];
if (distancia < distancias[vecino]) {
distancias[vecino] = distancia;
cola.enqueue(vecino, distancia);
}
}
}
}
return distancias;
}
// Ejemplo de uso
const grafo = {
'A': { 'B': 4, 'C': 2 },
'B': { 'A': 4, 'D': 3, 'E': 2 },
'C': { 'A': 2, 'D': 4 },
'D': { 'B': 3, 'C': 4, 'E': 3 },
'E': { 'B': 2, 'D': 3 }
};
const distancias = dijkstra(grafo, 'A');
console.log("Distancias desde A:", distancias);
Implementación en C++
C++ es un lenguaje muy utilizado en aplicaciones que requieren alta eficiencia, como videojuegos y sistemas en tiempo real. Aquí te dejo un ejemplo de cómo podrías implementar el algoritmo de Dijkstra en C++.
#include <iostream>
#include <vector>
#include <queue>
#include <unordered_map>
#include <limits>
using namespace std;
typedef pair<int, int> Par;
const int INF = numeric_limits<int>::max();
void dijkstra(unordered_map<int, vector<Par>> &grafo, int inicio) {
unordered_map<int, int> distancias;
for (const auto &nodo : grafo) {
distancias[nodo.first] = INF;
}
distancias[inicio] = 0;
priority_queue<Par, vector<Par>, greater<Par>> cola;
cola.push({0, inicio});
while (!cola.empty()) {
int distancia_actual = cola.top().first;
int nodo_actual = cola.top().second;
cola.pop();
if (distancia_actual > distancias[nodo_actual]) continue;
for (const auto &vecino : grafo[nodo_actual]) {
int distancia = distancia_actual + vecino.second;
if (distancia < distancias[vecino.first]) {
distancias[vecino.first] = distancia;
cola.push({distancia, vecino.first});
}
}
}
for (const auto &d : distancias) {
cout << "Distancia desde " << inicio << " hasta " << d.first << " es " << d.second << endl;
}
}
int main() {
unordered_map<int, vector<Par>> grafo;
grafo[1] = {{2, 4}, {3, 2}};
grafo[2] = {{1, 4}, {4, 3}, {5, 2}};
grafo[3] = {{1, 2}, {4, 4}};
grafo[4] = {{2, 3}, {3, 4}, {5, 3}};
grafo[5] = {{2, 2}, {4, 3}};
dijkstra(grafo, 1);
return 0;
}
Conclusión
El algoritmo de Dijkstra es una herramienta fundamental en el mundo de la informática y las matemáticas, con aplicaciones prácticas que van desde la navegación en mapas hasta la optimización de redes de telecomunicaciones. Aunque a primera vista puede parecer complejo, su lógica es bastante directa: encontrar el camino más corto en un grafo minimizando los costos. Gracias a su eficiencia y simplicidad, Dijkstra se ha convertido en un estándar para resolver problemas de rutas óptimas en diversos campos.
En este artículo, exploramos qué es el algoritmo de Dijkstra, para qué sirve, y cómo puedes implementarlo en diferentes lenguajes de programación. Además, visualizamos el funcionamiento del algoritmo paso a paso, lo que te ayudará a entenderlo mejor y aplicarlo en tus proyectos. Si te interesa profundizar en el mundo de los algoritmos y las estructuras de datos, el algoritmo de Dijkstra es un excelente punto de partida.
No dudes en experimentar con las implementaciones que te mostramos y en explorar otros algoritmos que también abordan el problema del camino más corto, como el algoritmo de Bellman-Ford o los algoritmos A*. ¡El aprendizaje continuo es la clave para dominar cualquier tema en informática!
Recursos adicionales
- Artículo de Wikipedia sobre el algoritmo de Dijkstra: Un excelente recurso para obtener una visión general y detallada del algoritmo.
- Visualización interactiva del algoritmo de Dijkstra: Una herramienta visual para ver el algoritmo en acción y entender su funcionamiento.
- GeeksforGeeks: Explicación detallada de Dijkstra: Un artículo con una explicación detallada y ejemplos de código.
- Coursera: Curso sobre grafos y algoritmos: Curso en línea que cubre el algoritmo de Dijkstra junto con otros algoritmos importantes en grafos.
- Video en YouTube: Dijkstra explicado paso a paso: Un video que desglosa el algoritmo de Dijkstra de manera clara y accesible.
- Udemy: Curso de algoritmos y estructuras de datos: Un curso completo que abarca Dijkstra y otros algoritmos esenciales.