Esquema general de AgentNet con aves interactuando y una red neuronal que modela sus dinámicas
Inteligencia Artificial

AgentNet: deep learning para entender el comportamiento de los sistemas complejos

Por Antonio Richaud , Publicado el 14 de noviembre de 2025

En muchos sistemas del mundo real que van desde bandadas de aves y cardúmenes de peces hasta partículas activas en la física observamos patrones colectivos claros, pero casi nunca conocemos las reglas microscópicas que los generan. El trabajo “Unraveling hidden interactions in complex systems with deep learning” propone AgentNet, la cual es una red neuronal diseñada para aprender esas reglas directamente a partir de puros datos.

AgentNet no solo predice cómo evoluciona un sistema con muchos agentes, si no que también es capaz de reconstruir la fuerza de interacción entre ellos usando atención neuronal. En este artículo vamos a desmenuzar cómo está construida, qué lo hace diferente a otros modelos de grafos, en qué sistemas se probó y por qué es tan importante en la unión entre deep learning y la física de sistemas complejos.

Introducción: cuando el caos tiene reglas

Si alguna vez has visto una bandada de aves girando, parece puro caos coordinado porque todas cambian de dirección casi al mismo tiempo, se abren, se cierran, forman remolinos. Pero atras de eso hay preguntas que siempre nos hacemos o almenos yo me hago:

  • ¿Cada ave a cuántas aves puede ver?
  • ¿Le importa más quien está enfrente o quien está atrás?
  • ¿Existe un radio máximo a partir del cual ya no se hacen caso?
  • ¿Todo eso se puede escribir como ecuaciones?

Ese tipo de preguntas no solo aplican a aves, también aparecen en el tráfico de coches, en redes sociales donde la gente se influencia con likes y comentarios, en experimentos de materia activa con partículas auto-propulsadas, o en colonias de bacterias que se organizan en patrones rarísimos.

La física tradicional suele atacar este problema con un enfoque “de arriba hacia abajo”: primero propones un modelo con ecuaciones y fuerzas, después ajustas parámetros con datos, para luego verificar si ese modelo reproduce el comportamiento global. El problema es que muchos sistemas reales son no lineales, ruidosos y de alta dimensión. A veces ni siquiera tienes idea de qué forma podrían tener las ecuaciones correctas.

El enfoque del artículo que estamos analizando va justo al revés: “Dame las trayectorias de todos los agentes en el tiempo y yo, red neuronal, aprendo por mí misma qué reglas podrían estar generando ese comportamiento. Y de paso te digo quién influye a quién y con qué fuerza.”

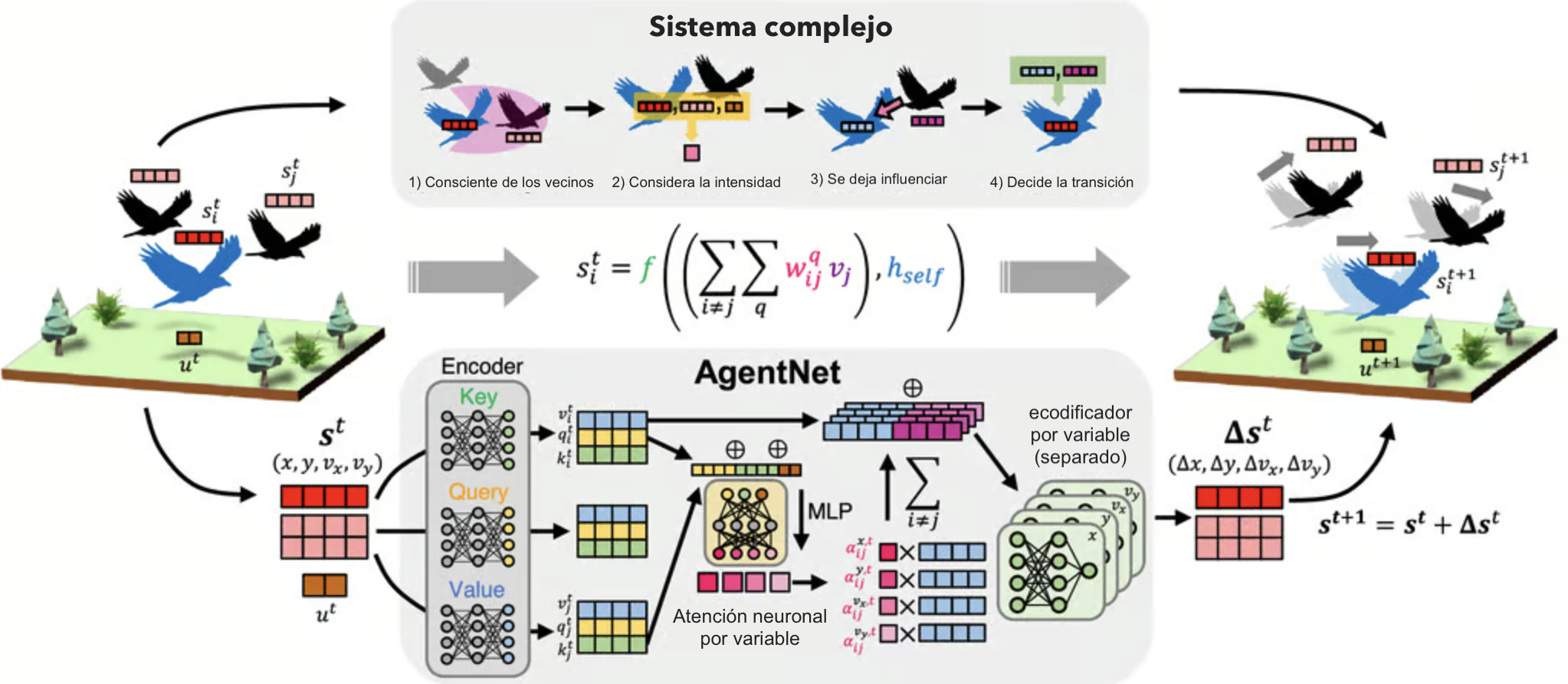
Esa red se llama AgentNet, y la portada que ves arriba es el mapa general de la historia: a la izquierda aparece el sistema físico (las aves), al centro el “cerebro” de AgentNet, y a la derecha la predicción del siguiente fotograma de la bandada.

¿Qué es AgentNet y qué problema resuelve?

La idea de AgentNet parte de algo muy simple: casi cualquier sistema de muchos componentes se puede ver como un grafo dinámico. Cada entidad (ave, partícula, coche, persona) se convierte en un nodo, y las posibles interacciones entre ellas se representan como aristas. Sobre este grafo, lo que nos interesa es describir cómo cambia el estado de cada nodo con el tiempo.

El estado de un agente i en el instante t se representa como un vector:

sit = (si,1t, si,2t, …, si,kt)

En ese vector puedes meter todo lo que defina al agente en ese momento como posición, velocidad, orientación, un estado binario “vivo/muerto”, etc. Además, el sistema puede tener variables globales compartidas por todos los agentes, que escribiremos como ut (por ejemplo, la temperatura o un parámetro de interacción).

El objetivo de AgentNet es aprender, directamente de los datos, la función que lleva el historial reciente de estados de cada agente al estado del siguiente paso:

{ …, sit-1, sit, ut } ⟶ sit+1

Para hacer el problema manejable, el modelo asume algo muy razonable en física de sistemas complejos: la dinámica está dominada por interacciones de pares. Es decir, lo que le sucede a un agente i se puede descomponer en: (1) su dinámica interna y (2) la suma de las influencias de cada vecino j. En forma compacta, el cambio en su estado se escribe como:

Δsit+1 = f( h₍self₎(sit,…, ut,…), Σj ≠ i h₍pair₎(sit,…, sjt,…, ut,…) )

Dicho en cristiano: “Lo que le pasa al agente i es la suma de lo que él haría por sí solo más la influencia combinada de todos sus vecinos”. En lugar de adivinar a mano las funciones hself y hpair, AgentNet las aproxima con redes neuronales organizadas como una Graph Neural Network (GNN).

Arquitectura general: encoder, atención y decoder

La arquitectura de AgentNet sigue un esquema de tres bloques: encoder → atención en el grafo → decoder. Cada bloque cumple una función específica:

  • El encoder toma el estado crudo de cada agente (y, cuando hace falta, su historial temporal) y lo convierte en un embedding interno mediante redes tipo MLP o LSTM.
  • El bloque de atención sobre el grafo decide cuánto influye cada vecino j sobre el agente objetivo i, produciendo pesos de interacción que dependen de sus estados.
  • El decoder combina la información propia del agente y la información agregada de sus vecinos para producir el cambio de estado Δsit+1 (por ejemplo, cuánto cambian su posición y su velocidad).

En la primera imagen que te aparecio al abrir este articulo hay un diagrama de este flujo: las aves en el paisaje representan a los agentes, el bloque central es AgentNet recibiendo sus estados y la escena de la derecha muestra la predicción del siguiente fotograma.

Atención por variable: la clave física de AgentNet

Muchas redes con atención para grafos (como las Graph Attention Networks clásicas) asignan un único peso escalar de importancia por vecino. Eso está bien para tareas de clasificación o recomendación, pero se queda corto para sistemas físicos donde cada componente del estado puede tener un alcance de interacción distinto.

Por ejemplo, una partícula puede “sentir” muy localmente la posición de sus vecinas, pero alinearse con sus velocidades en una escala algo mayor. Meter todo eso en un solo número borra muchos detalles.

AgentNet resuelve esto con un truco bien ingenioso: en lugar de un peso por vecino, calcula un peso de atención diferente para cada variable del estado. Para cada par de agentes (i, j) y para cada componente q del vector de estado (por ejemplo x, y, vx, vy), el modelo aprende un peso αijq:

αijq = σ(aijq)

donde aijq es un puntaje calculado por un pequeño MLP a partir de los embeddings de los agentes i y j (más, si aplica, las variables globales), y σ(·) es una función sigmoide que lo lleva al rango (0, 1). De esta manera, αijq se puede interpretar como “qué tanto siente el agente i al agente j en la variable q”.

Luego, AgentNet usa esos pesos para construir un “mensaje” agregado desde los vecinos hacia el agente objetivo, y pasa ese mensaje por decodificadores separados por variable. Eso obliga a que la contribución en posición se mantenga separada de la contribución en velocidad, y es justamente lo que permite que, más adelante, los mapas de atención se parezcan muchísimo a fuerzas físicas reales en los sistemas que estudian.

Cómo se entrena AgentNet y qué produce exactamente

Hasta aquí nada más hemos visto qué representa AgentNet y cómo usa la atención por variable para medir la influencia entre agentes. Falta responder dos preguntas muy prácticas: ¿qué es exactamente lo que predice el modelo? y ¿cómo se entrena para que eso tenga sentido físico?

Historial de estados

En los sistemas más sencillos, basta con suponer que el siguiente estado solo depende del instante actual, es una dinámica Markoviana. Pero muchos sistemas reales tienen memoria, o sea que, el comportamiento de hoy depende de lo que pasó hace varios pasos.

Para capturar esto, AgentNet no mira solo el estado actual sit, sino una ventana temporal de tamaño m:

sit,m = (sit-m+1, …, sit-1, sit)

Ese historial pasa por el encoder. Cuando la memoria es importante (como en partículas activas con fuerzas persistentes), el encoder se implementa con una LSTM que comprime toda la historia en un solo embedding por agente. En sistemas sin tanta memoria basta con un MLP que procese el estado actual.

Salida del modelo

AgentNet no suele predecir directamente el estado completo sit+1, sino el cambio respecto al paso anterior:

Δsit = (Δx, Δy, Δvx, Δvy, …)

y luego actualiza con la regla simple:

sit+1 = sit + Δsit

En los ejemplos más deterministas, como el autómata celular tipo Juego de la Vida,, el decoder produce directamente el valor siguiente de cada variable o la probabilidad de cada estado discreto. En sistemas continuos y ruidosos, como partículas o aves, el modelo da un paso más y predice distribuciones, no solo valores puntuales.

Para cada componente relevante del estado (por ejemplo, las coordenadas x, y o las velocidades), el decoder saca los parámetros de una Gaussiana 1D:

(μq, σq) para cada variable q ∈ {x, y, vx, vy, …}

Con eso puedes obtener tanto una trayectoria “promedio” (usando μ) como trayectorias muestreadas que reflejen la incertidumbre del sistema, algo importante cuando el ruido y el caos juegan un papel central.

Función de pérdida

La forma de entrenar AgentNet depende del tipo de variables que esté prediciendo:

  • En sistemas discretos (por ejemplo, “viva/muerta” en un autómata celular), se usa entropía cruzada entre la distribución que predice el modelo y el estado real observado.
  • En sistemas continuos y ruidosos, se minimiza la log-verosimilitud negativa de las Gaussianas anteriores, o sea que, cuanto más cerca esté la muestra real de la distribución que propone el modelo, menor es la pérdida.

El entrenamiento se hace con optimizadores tipo Adam, usando lotes de trayectorias y generando predicciones de manera autoregresiva, lo que significa que la salida de un paso se alimenta como entrada del siguiente. De esta forma, AgentNet no solo aprende a acertar un paso aislado, sino a mantener trayectorias coherentes en el tiempo.

Con esta base ya estamos listos para ver lo más divertido: qué descubre AgentNet cuando la soltamos sobre distintos sistemas, desde simulaciones clásicas hasta datos reales de bandadas de aves.

Qué descubre AgentNet en distintos sistemas

Con la arquitectura sobre la mesa, viene la parte más divertida, que es: ver qué descubre AgentNet cuando la soltamos sobre sistemas donde sí conocemos las reglas (para verificar que las recupera) y sobre un sistema real donde las reglas son desconocidas, como las bandadas de aves.

Los autores prueban el modelo en cuatro escenarios:

  • Un autómata celular tipo Juego de la Vida.
  • El modelo de Vicsek de partículas alineadas (bandadas sintéticas).
  • Un sistema de partículas activas AOUP con memoria.
  • Trayectorias 3D de bandadas reales de vencejos de chimenea.

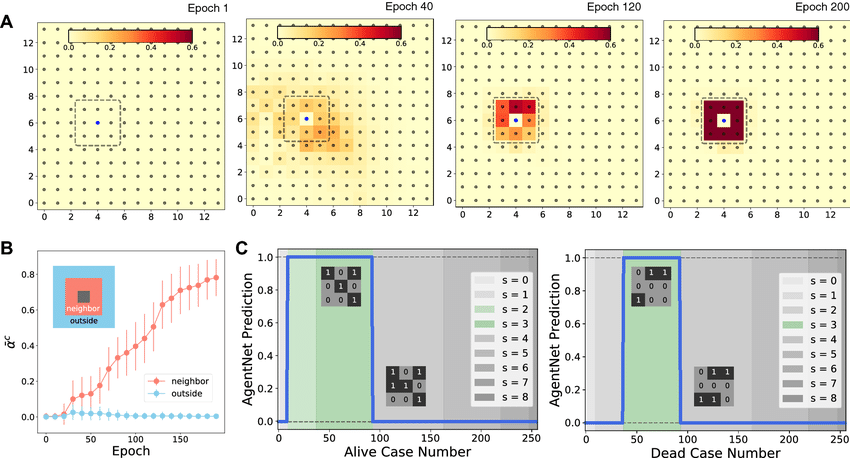
Autómata celular: redescubriendo el Juego de la Vida

El primer experimento es un clásico: un autómata celular binario similar al Juego de la Vida. Cada celda puede estar “viva” o “muerta” y su estado futuro depende de las ocho celdas vecinas, la llamada vecindad de Moore.

AgentNet ve la cuadrícula como un conjunto de agentes con su posición (x, y) y estado c ∈ {0, 1}. El trabajo consiste en predecir el estado en el siguiente paso para cada celda, a partir de configuraciones iniciales aleatorias.

Sin decirle nada sobre “vecindarios” ni sobre reglas lógicas, el modelo empieza con una atención dispersa y, a medida que entrena, la atención de cada celda se va concentrando justo en las ocho celdas adyacentes. Al final, AgentNet reproduce con precisión las reglas del autómata y alcanza una exactitud prácticamente perfecta en los estados futuros.

Resultados de AgentNet en un autómata celular tipo Juego de la Vida, mostrando la evolución de los pesos de atención y la precisión del modelo
Figura 1. AgentNet aplicado a un autómata celular tipo Juego de la Vida. Arriba: la atención de una celda se concentra progresivamente en sus 8 vecinos inmediatos. Abajo: precisión del modelo para los estados “vivo” y “muerto” frente a las reglas reales.

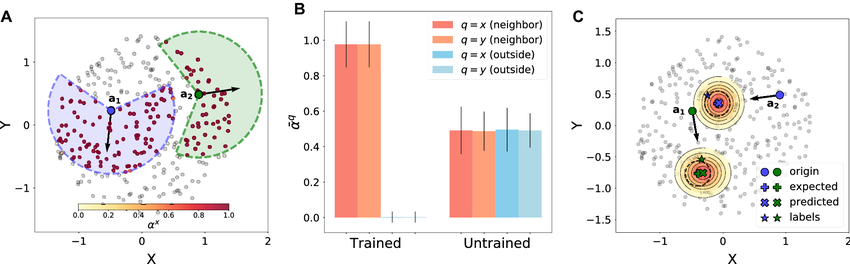
Modelo de Vicsek: bandadas sintéticas y campo visual

El siguiente test es el modelo de Vicsek, muy usado para estudiar materia activa. Aquí cada partícula se mueve con velocidad constante y actualiza su dirección alineándose con sus vecinas dentro de un cierto radio y dentro de un ángulo de visión frontal.

De forma simplificada, la actualización de la dirección se puede escribir como:

θit+1 = arg(Σj ∈ N(i) ei θjt) + ηit

donde N(i) son los vecinos dentro del radio de interacción, y ηit es un término de ruido. En los experimentos, cada agente tiene un radio de interacción fijo y un campo visual limitado: solo “ve” a los que están más o menos enfrente.

AgentNet recibe como entrada las posiciones y velocidades de las partículas y debe predecir sus posiciones futuras. Después del entrenamiento, los mapas de atención muestran algo muy claro: cada agente pone atención alta solo a partículas cercanas y dentro de un cono frontal, y prácticamente ignora a las demás. Es decir, recupera tanto el radio como el ángulo de visión del modelo de Vicsek.

Resultados de AgentNet en el modelo de Vicsek, mostrando agentes, rango de interacción y patrones de atención en forma de cono frontal
Figura 2. Resultados de AgentNet en el modelo de Vicsek. A la izquierda: agentes con su radio de interacción. A la derecha: patrones de atención que forman un cono frontal, reflejando tanto el radio como el ángulo de visión de los vecinos relevantes.

AOUP: partículas activas con memoria y fuerzas efectivas

El tercer escenario es más exigente, un sistema de partículas activas Ornstein–Uhlenbeck (AOUP). Aquí cada partícula está sometida a varios tipos de fuerzas:

  • Un potencial externo que la confina.
  • Un potencial interno de interacción suave con las demás partículas.
  • Ruido térmico.
  • Una fuerza activa que tiene memoria en el tiempo.

Una ecuación típica de este modelo (en versión simplificada y sobreamortiguada) se escribe como:

γ · ẋi = Fiext + Fiint + √(2γT) · ηi + γ fi

donde la fuerza activa fi sigue un proceso de Ornstein–Uhlenbeck:

τ · ḟi = − fi + √(2Da) · wi

En este caso, AgentNet recibe como entrada varios pasos del historial de posición y velocidad de cada partícula, además de un parámetro global que controla el alcance de la interacción. El encoder usa una LSTM para capturar la memoria, y el decoder produce las distribuciones gaussianas de posición y velocidad futuras.

Los resultados muestran que AgentNet no solo predice trayectorias con menos error que modelos base (extrapolación lineal, LSTM puro o GAT), sino que la atención promedio se alinea casi linealmente con la fuerza interna real derivada del potencial. Es decir, la atención variable por componente se comporta, hasta un factor de escala, como una fuerza efectiva entre partículas.

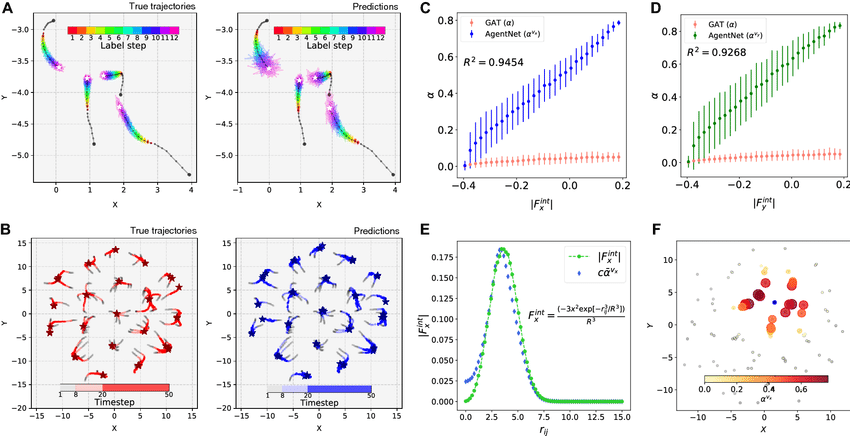
Resultados de AgentNet en el sistema AOUP, mostrando trayectorias, correlación entre atención y fuerza interna, y mapas espaciales de la interacción
Figura 3. AgentNet en un sistema AOUP. Arriba: trayectorias reales y trayectorias predichas. Centro: relación casi lineal entre atención promedio y fuerza interna en cada componente. Abajo: fuerza interna promedio en función de la distancia y mapas espaciales que reflejan cómo crece y se apaga la interacción.

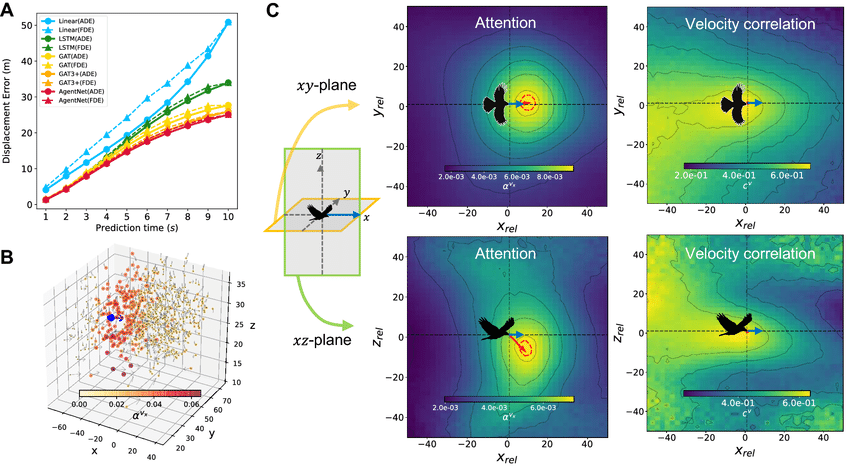
Bandadas reales de vencejos de chimenea

El último escenario es el más cercano al mundo real, bandadas de vencejos de chimenea volando alrededor de un edificio antes de entrar a dormir. A partir de múltiples cámaras de alta velocidad, se reconstruyen trayectorias 3D de cientos de aves durante unos segundos.

Aquí el reto ya no es solo la dinámica compleja de las aves, sino que aparecen y desaparecen del campo de visión, las trayectorias están llenas de oclusiones y la cantidad de agentes puede variar de unas pocas centenas a más de mil en una misma escena.

Para manejarlo, los autores adaptan AgentNet para trabajar con un grafo dinámico donde los nodos pueden nacer y morir en el tiempo, manteniendo estados ocultos coherentes para cada ave mientras está visible.

De nuevo, el modelo recibe la posición y la velocidad de cada ave y predice distribuciones futuras. AgentNet logra errores de desplazamiento menores que extrapolaciones simples y que otros modelos recurrentes y de grafos, pero lo más interesante son los mapas de atención:

  • Cada ave presta más atención a vecinas cercanas y en la parte frontal.
  • El patrón promedio de atención, alineado por la dirección de vuelo, se parece a un cono visual frontal y ligeramente hacia abajo.
  • La correlación de velocidades entre aves, en cambio, es mucho más difusa y simétrica.

Esto sugiere que la atención de AgentNet está capturando algo muy cercano al campo visual efectivo de las aves y no solo una correlación estadística. Es una especie de “radiografía funcional” de cómo cada individuo decide a quién hacerle caso dentro de la bandada.

Resultados de AgentNet en bandadas reales de vencejos de chimenea, mostrando errores de desplazamiento, una escena 3D con atención y mapas promedio de atención frente a correlación de velocidades
Figura 4. AgentNet aplicado a bandadas reales de vencejos de chimenea. Izquierda: error de desplazamiento frente a modelos base. Centro: escena 3D con la atención de un ave objetivo sobre sus vecinas. Derecha: mapas promedio de atención (arriba) y de correlación de velocidades (abajo), revelando un cono de interacción frontal y ligeramente hacia abajo.

En resumen, AgentNet no nada más es una red neuronal más, sino que es una propuesta seria para usar deep learning como herramienta de descubrimiento en sistemas complejos, en lugar de imponer las reglas desde la teoría, dejamos que el modelo las infiera a partir de los datos y luego las leemos de vuelta a través de la atención.

Fuentes y recursos para profundizar