Inteligencia Artificial

Redes perceptrón multicapa (MLP): ¿Qué son, cómo funcionan y cuándo utilizarlas? (o no)

Por Antonio Richaud, Publicado el 18 de Octubre de 2024

Las redes perceptrón multicapa (MLP) son un tipo de red neuronal artificial que ha desempeñado un papel super importantisimo en el desarrollo del aprendizaje profundo. Si bien no son las arquitecturas más recientes o sofisticadas, los MLP han sido fundamentales para resolver problemas de clasificación y regresión desde sus inicios, y aún se utilizan en muchos contextos debido a su simplicidad y versatilidad.

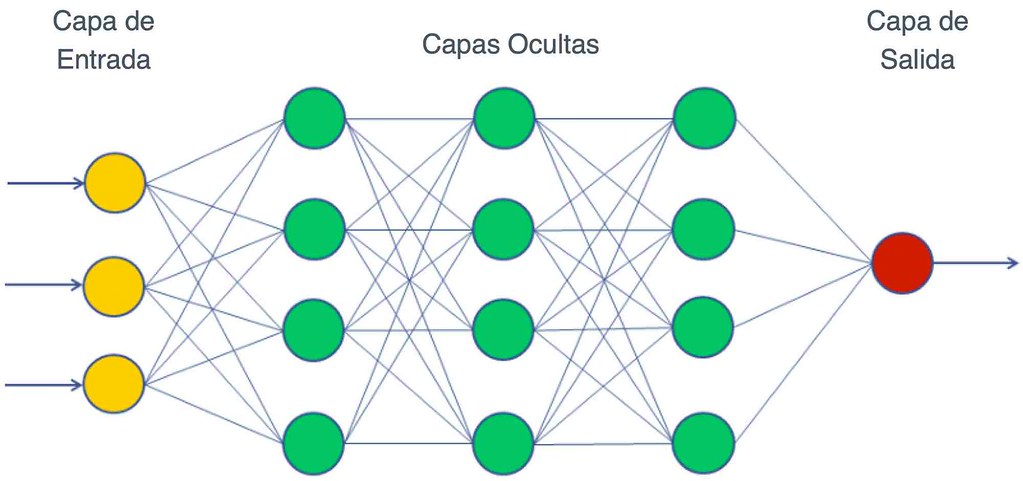
Un MLP se compone de varias capas de neuronas organizadas en tres tipos principales: capa de entrada, capas ocultas y capa de salida. Cada neurona en estas capas está conectada a otras mediante pesos que se ajustan durante el proceso de aprendizaje para mejorar la precisión del modelo. A través de funciones de activación como ReLU y Sigmoid, los MLP pueden resolver problemas que involucran relaciones no lineales en los datos.

Sin embargo, a pesar de su utilidad, los MLP tienen sus limitaciones, especialmente cuando se trata de manejar datos más complejos como imágenes o secuencias temporales. En este artículo, exploraremos cómo funcionan los MLP, sus aplicaciones más comunes, y analizaremos cuándo es recomendable utilizarlos y cuándo otras arquitecturas neuronales, como las redes convolucionales o las redes recurrentes, son más adecuadas.

Arquitectura de un Perceptrón Multicapa

Un perceptrón multicapa (MLP) se organiza en tres tipos de capas: la capa de entrada, una o más capas ocultas y la capa de salida. Cada una de estas capas tiene un papel específico dentro de la red neuronal, y su interacción permite a los MLPs aprender patrones complejos en los datos.

1. Capa de entrada

La capa de entrada es el punto donde los datos crudos ingresan a la red. Cada nodo de esta capa representa una característica o variable del conjunto de datos. Por ejemplo, si tenemos un conjunto de datos con tres características (como el nivel de oscuridad de una habitación, la hora del día y la presencia de personas), la capa de entrada tendría tres nodos, uno para cada característica.

2. Capas ocultas

Las capas ocultas son donde ocurre el aprendizaje profundo. Cada nodo en estas capas toma los valores de la capa anterior, los multiplica por pesos y los pasa a través de una función de activación, como ReLU (Rectified Linear Unit) o Sigmoid. Estas capas permiten a los MLPs aprender relaciones no lineales en los datos. El número de capas ocultas y de nodos por capa es un parámetro ajustable que depende de la complejidad del problema.

3. Capa de salida

La capa de salida proporciona el resultado final de la red, ya sea una clasificación o una predicción. Por ejemplo, en el caso de predecir si encender o no una luz, la capa de salida daría un valor de 0 o 1, dependiendo de los valores procesados en las capas ocultas. La función de activación de esta capa generalmente es Sigmoid para problemas binarios o Softmax cuando hay múltiples clases a predecir.

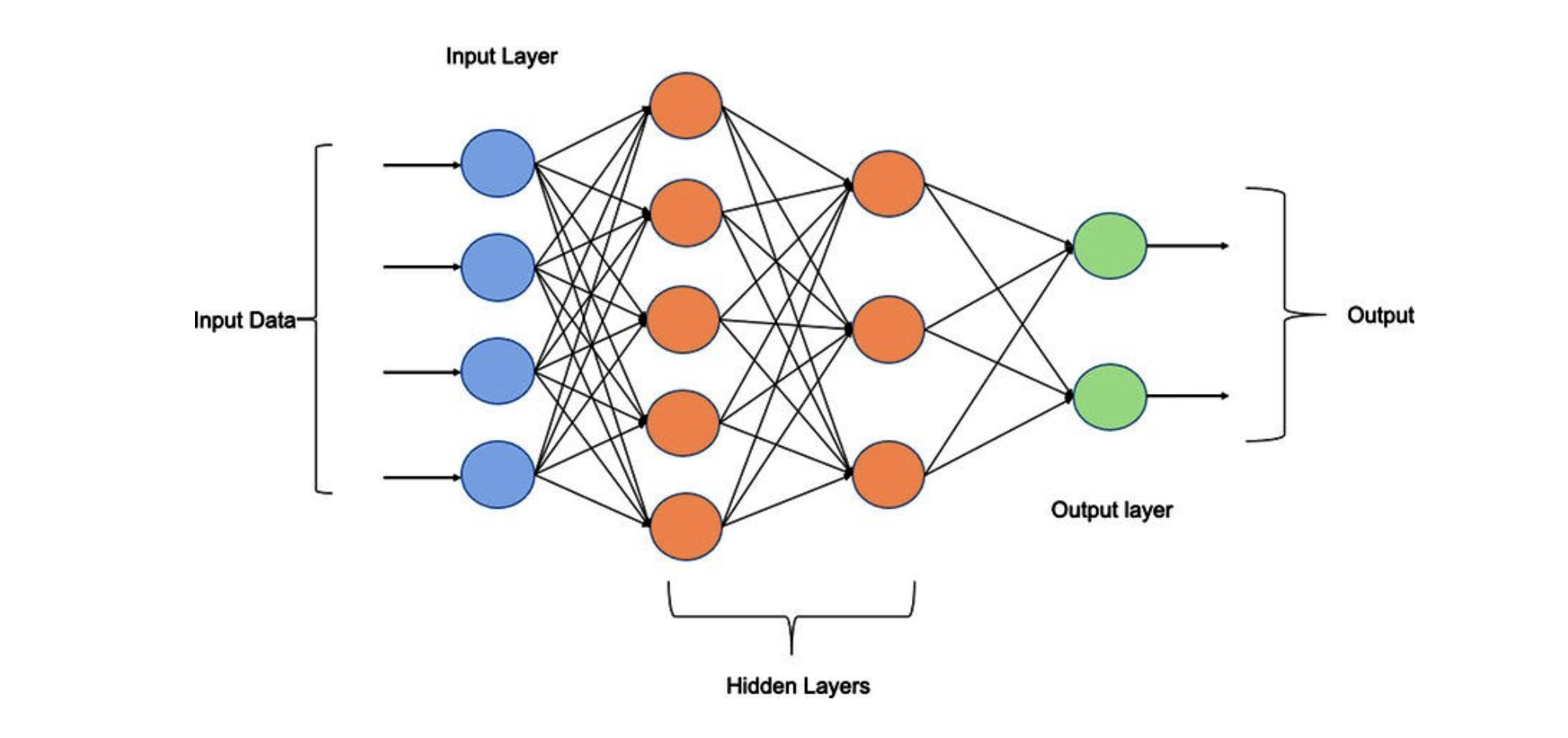
Diagrama de un MLP básico — Figura 1: Diagrama de un perceptrón multicapa (MLP) con una capa de entrada, dos capas ocultas y una capa de salida.

Ciclo de procesamiento de datos en un MLP

El proceso de un perceptrón multicapa (MLP) implica tomar datos de entrada, procesarlos a través de una serie de cálculos en las capas ocultas y finalmente generar una predicción o decisión en la capa de salida. Este ciclo de procesamiento se realiza mediante pesos, funciones de activación y ajustes que permiten que el modelo aprenda de los datos de manera eficiente.

1. Paso a paso: procesamiento de una predicción

Para ilustrar cómo funciona el procesamiento de datos en un MLP, consideremos un ejemplo práctico: predecir si encender o no una luz basada en tres factores clave:

Nivel de oscuridad de la habitación (x1): valor entre 0 (muy iluminada) y 1 (muy oscura).
Hora del día (x2): valor entre 0 (mañana) y 1 (noche).
Presencia de personas (x3): valor entre 0 (sin personas) y 1 (personas presentes).

Supongamos que tenemos los siguientes valores:

Oscuridad de la habitación (x1): 0.9
Hora del día (x2): 0.8
Presencia de personas (x3): 1.0

2. Cálculos en las capas ocultas

Estos valores se multiplican por pesos asignados a cada conexión entre los nodos. Para simplificar, tomemos los siguientes pesos y sesgos para las dos neuronas en la primera capa oculta:

h1 = ReLU(0.9 × 0.5 + 0.8 × 0.2 + 1.0 × 0.8 − 0.1) h2 = ReLU(0.9 × 0.9 + 0.8 × 0.7 + 1.0 × 0.3 + 0.2)

Tras calcular las salidas de las neuronas en la capa oculta usando la función de activación ReLU, estas se convierten en las entradas para la siguiente capa.

3. Cálculos en la capa de salida

Los valores resultantes de las capas ocultas se transmiten a la capa de salida, donde nuevamente se aplican pesos y una función de activación. En este caso, se usa la función Sigmoid para obtener un valor de salida entre 0 y 1:

o = Sigmoid(1.31 × 1.2 + 1.87 × 0.5 − 0.3) o ≈ 0.90

Dado que la salida es 0.90, que está cerca de 1, el modelo decide que la luz debe encenderse. Este tipo de cálculo se repite para cada conjunto de datos de entrada, y el modelo ajusta sus pesos mediante el proceso de aprendizaje para mejorar la precisión de sus predicciones.

Matemáticas detrás de los MLPs

Los perceptrones multicapa (MLP) dependen de cálculos matemáticos precisos para transformar las entradas en predicciones útiles. Estos cálculos involucran principalmente la multiplicación de los valores de entrada por pesos y la suma de sesgos, seguidos de la aplicación de funciones de activación. Aquí desglosamos las matemáticas que ocurren dentro de cada neurona y su importancia para el funcionamiento del MLP.

1. Cálculos en una neurona

Cada neurona en una capa toma las entradas de la capa anterior, las multiplica por pesos y agrega un sesgo (bias). Esta suma ponderada se transforma usando una función de activación, que introduce no linealidades en el modelo. La fórmula básica es:

z = (x1 × w1) + (x2 × w2) + ... + (xn × wn) + b

Donde:

x1, x2, ... xn: son los valores de entrada.
w1, w2, ... wn: son los pesos asignados a cada conexión.
b: es el sesgo de la neurona.
z: es el valor ponderado antes de aplicar la función de activación.

2. Función de activación

Una vez que la neurona calcula el valor z, este pasa por una función de activación. Las dos funciones más comunes en los MLPs son:

ReLU (Rectified Linear Unit): Devuelve 0 si el valor es negativo, y el valor original si es positivo. f(z) = max(0, z)
Sigmoid: Convierte el valor en un número entre 0 y 1, útil para clasificación binaria. f(z) = 1 / (1 + e^-z)

La función de activación es crucial porque introduce no linealidades en el modelo, permitiendo que el MLP aprenda patrones complejos que no pueden ser resueltos por modelos lineales simples.

Gráfico de funciones de activación ReLU y Sigmoid — Figura 2: Comparación de las funciones de activación ReLU y Sigmoid.

3. Ejemplo numérico: Cálculo completo

Supongamos que tenemos una neurona en una capa oculta con los siguientes valores de entrada y pesos:

x1 = 0.9, w1 = 0.5
x2 = 0.8, w2 = 0.2
x3 = 1.0, w3 = 0.8
Sesgo (b) = -0.1

El valor z en esta neurona sería:

z = (0.9 × 0.5) + (0.8 × 0.2) + (1.0 × 0.8) − 0.1 z = 1.31

Aplicando la función de activación ReLU:

f(z) = max(0, 1.31) = 1.31

Este valor se transmitirá a la siguiente capa del MLP, donde seguirá el mismo proceso hasta llegar a la capa de salida.

Funciones de activación en MLPs

Las funciones de activación son fundamentales para el funcionamiento de los perceptrones multicapa (MLP). Permiten que las redes neuronales aprendan relaciones no lineales, lo que las hace mucho más poderosas que los modelos lineales. Sin estas funciones, las capas ocultas no tendrían un impacto significativo en los cálculos, y la red no podría aprender patrones complejos.

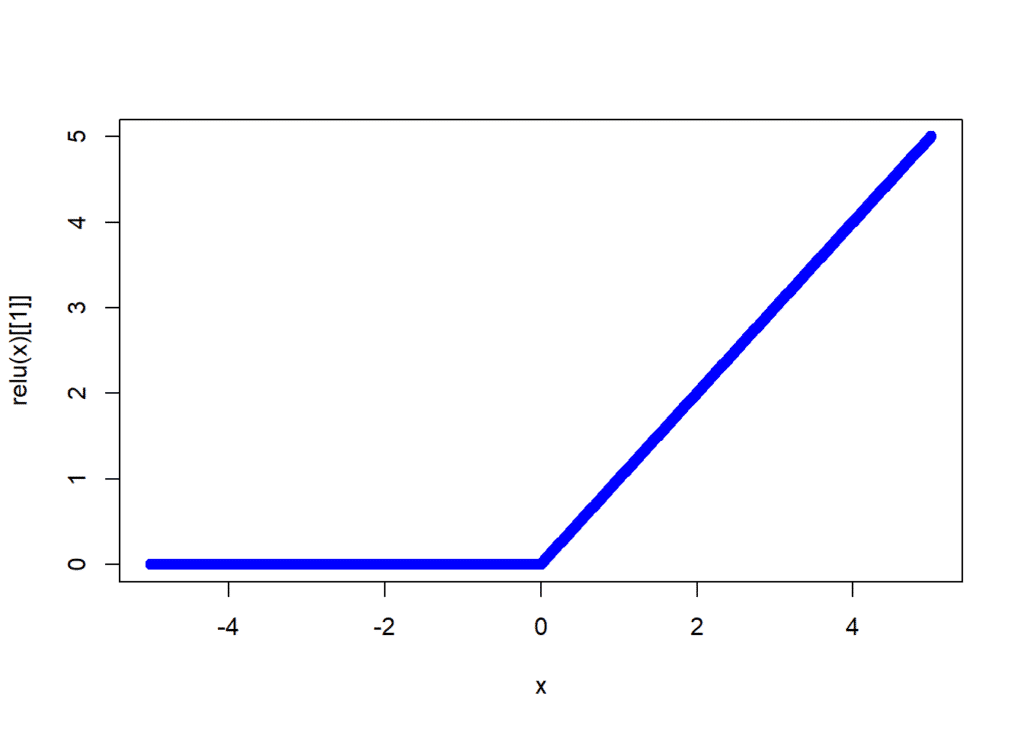
1. ReLU (Rectified Linear Unit)

La función ReLU (Rectified Linear Unit) es una de las más utilizadas debido a su simplicidad y efectividad. ReLU devuelve el valor original si es positivo y 0 si es negativo. Esto permite que la red sea eficiente computacionalmente, evitando complicaciones derivadas de gradientes pequeños.

f(z) = max(0, z)

ReLU es especialmente útil en capas ocultas, ya que introduce no linealidades sin saturar los valores, lo que ocurre en otras funciones como Sigmoid. Sin embargo, tiene el problema de que valores negativos permanecen sin activarse, lo que puede resultar en la "muerte" de algunas neuronas.

Figura 3: Gráfico de la función ReLU, que devuelve 0 para valores negativos y el valor original para valores positivos.

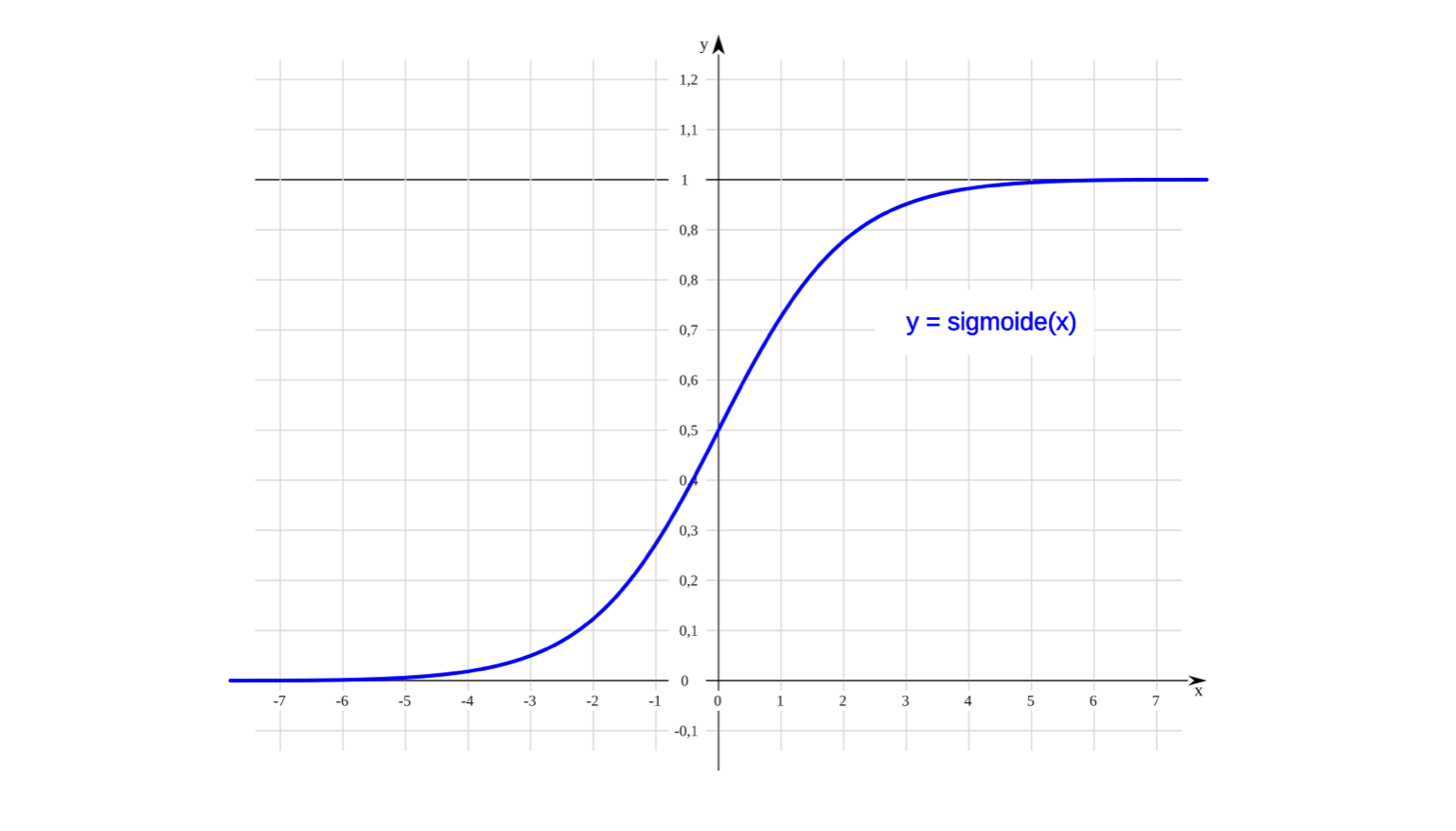
2. Sigmoid

La función Sigmoid es comúnmente utilizada en la capa de salida de los MLPs para tareas de clasificación binaria. Convierte el valor de entrada en un número entre 0 y 1, lo que la hace útil cuando se necesita una probabilidad como salida.

f(z) = 1 / (1 + e^-z)

Si bien es útil en las capas de salida, la función Sigmoid tiende a saturar los valores cuando el valor de entrada es muy alto o muy bajo, lo que puede ralentizar el aprendizaje en las capas ocultas. Este problema es conocido como el desvanecimiento del gradiente.

Figura 4: Gráfico de la función Sigmoid, que convierte valores en un rango entre 0 y 1, comúnmente usada en clasificación binaria.

3. Tanh (Tangente hiperbólica)

La función Tanh es similar a la Sigmoid, pero escala los valores entre -1 y 1. Esto le permite centrarse en un rango más amplio de valores en lugar de restringirlos únicamente a positivos, lo que puede mejorar el rendimiento en ciertas tareas.

f(z) = (e^z - e^-z) / (e^z + e^-z)

Tanh es una opción común en las capas ocultas cuando se busca mejorar la diferenciación entre valores positivos y negativos. Al igual que Sigmoid, puede sufrir de problemas de desvanecimiento del gradiente cuando el valor absoluto de la entrada es grande.

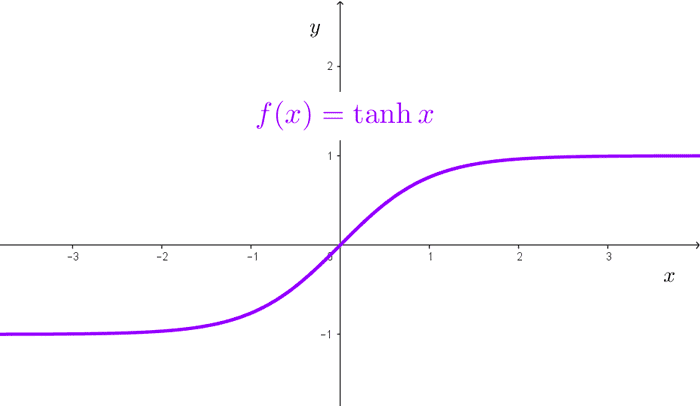
Figura 5: Gráfico de la función Tanh, que convierte los valores entre -1 y 1, ampliando el rango de salida comparado con Sigmoid.

4. ¿Cuál función de activación elegir?

La elección de la función de activación depende en gran medida de la tarea que se esté resolviendo. En capas ocultas, ReLU es una de las opciones más populares debido a su simplicidad y eficiencia. Para las capas de salida, Sigmoid se prefiere en problemas de clasificación binaria, mientras que Softmax es más adecuado para clasificación multiclase.

Sin embargo, las funciones de activación más complejas, como Tanh, pueden ser útiles en capas intermedias cuando se necesita una mayor diferenciación entre valores negativos y positivos. La elección correcta puede influir significativamente en el rendimiento del modelo y la velocidad de convergencia durante el entrenamiento.

Limitaciones de los MLPs y alternativas recomendadas

Aunque los perceptrones multicapa (MLP) son modelos poderosos para muchos tipos de problemas, también tienen limitaciones significativas que los hacen inadecuados para ciertas tareas más complejas. Estas limitaciones surgen debido a la naturaleza misma de su arquitectura y la forma en que procesan los datos.

1. Limitaciones de los MLPs

Datos no estructurados: Los MLPs no son efectivos para trabajar con datos no estructurados como imágenes, audio o texto sin preprocesamiento extensivo. No pueden capturar patrones espaciales o secuenciales de manera eficiente.
Profundidad y sobreajuste: A medida que los MLPs se vuelven más profundos (es decir, con más capas ocultas), pueden aprender patrones muy específicos de los datos de entrenamiento, lo que los hace susceptibles al sobreajuste si no se utilizan técnicas adecuadas de regularización.
Coste computacional: Entrenar un MLP profundo puede ser computacionalmente costoso y lento, especialmente cuando el número de neuronas y capas aumenta.
Incapacidad para captar relaciones temporales: Los MLPs no tienen memoria interna, por lo que no pueden capturar dependencias temporales en secuencias de datos, como en series temporales o procesamiento de lenguaje natural.

2. Alternativas recomendadas para casos específicos

Existen otras arquitecturas de redes neuronales que son más adecuadas que los MLPs para ciertos tipos de datos y problemas específicos. A continuación, se presentan algunas de las más utilizadas:

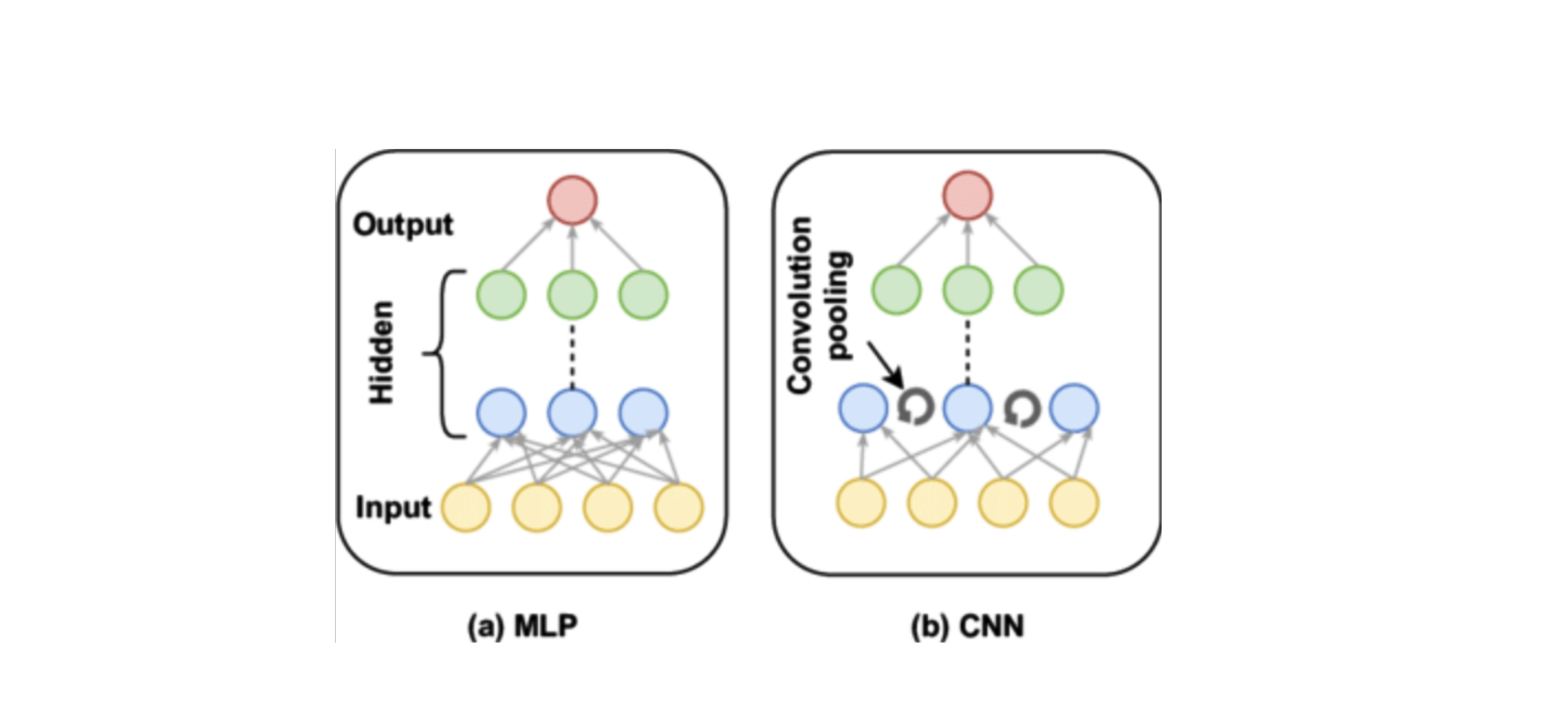
a) Redes Neuronales Convolucionales (CNNs) para datos espaciales

Las redes neuronales convolucionales (CNN) están diseñadas para capturar relaciones espaciales en los datos, lo que las hace ideales para tareas como el reconocimiento de imágenes, donde los píxeles tienen una relación espacial entre sí. Las CNNs usan capas convolucionales para identificar características importantes (como bordes, texturas y patrones) que los MLPs no pueden captar eficientemente.

Comparación entre CNN y MLP — Figura 6: Comparación entre el procesamiento de una CNN y un MLP en imágenes.

b) Redes Neuronales Recurrentes (RNNs) para datos secuenciales

Las redes neuronales recurrentes (RNN) están diseñadas para manejar secuencias de datos, ya que pueden mantener una memoria interna que les permite recordar información previa en la secuencia. Esto es útil en problemas como la predicción de series temporales y el procesamiento de lenguaje natural. Extensiones de las RNN, como las LSTM (Long Short-Term Memory), mejoran la capacidad de la red para capturar dependencias a largo plazo.

c) Transformers para modelos de lenguaje y procesamiento secuencial

Los transformers son una arquitectura más reciente que ha superado a las RNNs en varias tareas relacionadas con el procesamiento de secuencias, particularmente en el procesamiento del lenguaje natural. Utilizan mecanismos de atención para identificar las relaciones entre las palabras de una secuencia, permitiendo una mayor eficiencia y precisión en tareas como la traducción automática y el análisis de sentimientos.

3. ¿Cuándo elegir un MLP y cuándo otras arquitecturas?

La elección de la arquitectura depende del tipo de problema que se esté resolviendo. Los MLPs son adecuados cuando se trabaja con datos tabulares y tareas de clasificación o regresión sencillas. Sin embargo, para tareas que involucren datos espaciales (como imágenes) o secuenciales (como texto o series temporales), es recomendable usar arquitecturas más avanzadas como CNNs, RNNs o Transformers.

En resumen, los MLP siguen siendo útiles en ciertos contextos, pero las necesidades actuales en el campo de la inteligencia artificial requieren soluciones más especializadas. Al conocer las fortalezas y debilidades de cada arquitectura, podemos seleccionar la más adecuada para cada tarea específica.

Conclusión

Las redes perceptrón multicapa (MLP) han sido una pieza fundamental en el desarrollo del aprendizaje profundo. Con su capacidad para aprender patrones complejos y no lineales, los MLPs son ideales para tareas de clasificación y regresión en datos tabulares y estructurados. Su simplicidad y capacidad de ser implementados en una variedad de contextos han hecho que se mantengan relevantes a lo largo del tiempo.

Sin embargo, como hemos explorado, los MLPs tienen limitaciones que los hacen menos efectivos en problemas que involucran datos espaciales o secuenciales, como imágenes, audio o lenguaje natural. En estos casos, otras arquitecturas neuronales más especializadas, como las redes neuronales convolucionales (CNNs), las redes recurrentes (RNNs) y los modelos basados en transformers, han demostrado ser superiores al capturar la estructura inherente en estos tipos de datos.

La elección de la arquitectura adecuada depende en gran medida del problema a resolver. Mientras que los MLPs son una excelente opción para problemas simples y datos estructurados, en aplicaciones más complejas es esencial considerar arquitecturas más avanzadas para garantizar un rendimiento óptimo. Con la evolución de las redes neuronales, cada tipo de modelo tiene su lugar y utilidad, y es fundamental saber cuándo y cómo aplicar cada uno de ellos.

En resumen, los MLPs siguen siendo una herramienta poderosa para problemas específicos, pero la inteligencia artificial moderna exige la flexibilidad y capacidad de adaptación que ofrecen las arquitecturas más recientes. Conocer las limitaciones de los MLP y las alternativas disponibles es clave para elegir la mejor solución a cualquier desafío en el aprendizaje profundo.

Recursos adicionales

Para aquellos interesados en aprender más sobre los perceptrones multicapa (MLP) y otras arquitecturas neuronales, aquí hay algunos recursos adicionales que pueden ser de gran utilidad:

Curso sobre Redes Neuronales en Coursera: Neural Networks and Deep Learning de Andrew Ng en Coursera. Un curso introductorio que cubre los MLPs y otras arquitecturas fundamentales.
Repositorio de ejemplos en TensorFlow: TensorFlow Tutorials. Una colección de tutoriales que muestra cómo implementar redes neuronales, incluyendo MLPs, CNNs y RNNs.
Paper sobre Transformers: Attention is All You Need. Este es el paper original que introdujo los modelos de transformers, revolucionando el procesamiento del lenguaje natural.
Documentación de PyTorch: PyTorch Documentation. Una guía completa para trabajar con PyTorch, una de las librerías más populares para la implementación de redes neuronales.
Tutorial de MLP en scikit-learn: MLP Classifier en scikit-learn. Un tutorial que muestra cómo usar un MLP para tareas de clasificación supervisada utilizando la biblioteca scikit-learn.
Libro: Deep Learning de Ian Goodfellow: Deep Learning. Un libro completo y detallado sobre los fundamentos de redes neuronales y el aprendizaje profundo, escrito por expertos en el campo.

Estos recursos proporcionan una base sólida para aquellos que deseen profundizar en el mundo del aprendizaje profundo y explorar las diversas arquitecturas que lo componen, desde los MLPs hasta los transformers.